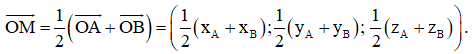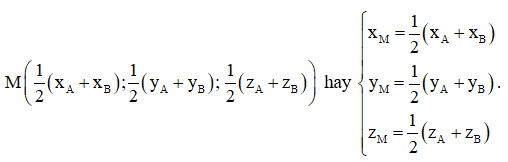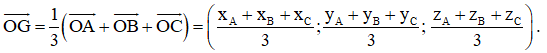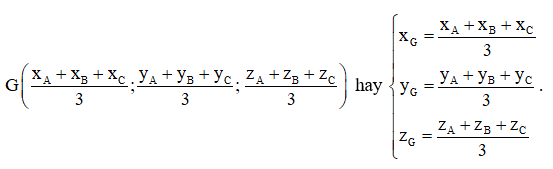Giải Toán 12 trang 75 Tập 1 Cánh diều

---

Với Giải Toán 12 trang 75 Tập 1 trong Bài 3: Biểu thức toạ độ của các phép toán vectơ Toán 12 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12 trang 75.

Giải Toán 12 trang 75 Tập 1 Cánh diều

Luyện tập 1 trang 75 Toán 12 Tập 1: a) Cho $\overrightarrow{u}=\left(-2;0;1\right),\overrightarrow{v}=\left(0;6;-2\right),\overrightarrow{w}=\left(-2;3;2\right)$. Tìm tọa độ của vectơ $\overrightarrow{u}+2\overrightarrow{v}-4\overrightarrow{w}$.

b) Cho ba điểm A(– 1; – 3; – 2), B(2; 3; 4), C(3; 5; 6). Chứng minh rằng ba điểm A, B, C thẳng hàng.

Lời giải:

a) Ta có $2\overrightarrow{v}=\left(0;12;-4\right),4\overrightarrow{w}=\left(-8;12;8\right)$ .

Do đó, $\overrightarrow{u}+2\overrightarrow{v}$ = (– 2 + 0; 0 + 12; 1 + (– 4)) = (– 2; 12; – 3).

Suy ra $\overrightarrow{u}+2\overrightarrow{v}-4\overrightarrow{w}$  = (– 2 – (– 8); 12 – 12; – 3 – 8).

Vậy $\overrightarrow{u}+2\overrightarrow{v}-4\overrightarrow{w}$  = (6; 0; – 11).

b) Ta có: $\overrightarrow{AB}$  = (2 – (– 1); 3 – (– 3); 4 – (– 2)) = (3; 6; 6),

               $\overrightarrow{AC}$  = (3 – (– 1); 5 – (– 3); 6 – (– 2)) = (4; 8; 8).

Ta có 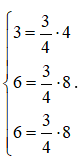 Từ đó suy ra $\overrightarrow{AB}=\frac{3}{4}\overrightarrow{AC}$.

Do đó, hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{AC}$ cùng phương.

Suy ra hai đường thẳng AB và AC song song hoặc trùng nhau, mà AB ∩ AC = A.

Vậy hai đường thẳng AB và AC trùng nhau hay ba điểm A, B, C thẳng hàng.

Hoạt động 2 trang 75 Toán 12 Tập 1: a) Trong không gian với hệ tọa độ Oxyz, cho hai điểm A(x_A; y_A; z_A) và B(x_B; y_B; z_B). Gọi M(x_M; y_M; z_M) là trung điểm của đoạn thẳng AB.

- Biểu diễn vectơ $\overrightarrow{OM}$ theo hai vectơ $\overrightarrow{OA}$ và $\overrightarrow{OB}$.

- Tính tọa độ của điểm M theo tọa độ của các điểm A(x_A; y_A; z_A) và B(x_B; y_B; z_B).

b) Trong không gian với hệ tọa độ Oxyz, cho tam giác ABC có trọng tâm G.

- Biểu diễn vectơ $\overrightarrow{OG}$ theo hai vectơ $\overrightarrow{OA}$, $\overrightarrow{OB}$ , $\overrightarrow{OC}$.

- Tính tọa độ của điểm G theo tọa độ của các điểm A(x_A; y_A; z_A), B(x_B; y_B; z_B), C(x_C; y_C; z_C).

Lời giải:

a)

- Vì M là trung điểm của AB nên với điểm O ta có: $\overrightarrow{OM}=\frac{1}{2}\left(\overrightarrow{OA}+\overrightarrow{OB}\right)$.

- Ta có A(x_A; y_A; z_A) và B(x_B; y_B; z_B) nên $\overrightarrow{OA}$ = (x_A; y_A; z_A) và $\overrightarrow{OB}$ = (x_B; y_B; z_B).

Khi đó, $\overrightarrow{OA}+\overrightarrow{OB}$  = (x_A + x_B; y_A + y_B; z_A + z_B).

Suy ra

Do đó,

b)

- Vì G là trọng tâm của tam giác ABC nên với điểm O ta có:

$\overrightarrow{OG}=\frac{1}{3}\left(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}\right)$.

- Ta có A(x_A; y_A; z_A), B(x_B; y_B; z_B), C(x_C; y_C; z_C).

Suy ra $\overrightarrow{OA}$ = (x_A; y_A; z_A), $\overrightarrow{OB}$  = (x_B; y_B; z_B), $\overrightarrow{OC}$ = (x_C; y_C; z_C).

Khi đó, $\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}$ = (x_A + x_B + x_C; y_A + y_B + y_C; z_A + z_B + z_C).

Suy ra 

Do đó,

Lời giải bài tập Toán 12 Bài 3: Biểu thức toạ độ của các phép toán vectơ hay khác:

• Giải Toán 12 trang 74

• Giải Toán 12 trang 76

• Giải Toán 12 trang 80

• Giải Toán 12 trang 81