Giải Toán 12 trang 44 Tập 2 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm lời giải bài tập Toán 12 trang 44 Tập 2 trong Bài 2: Phương trình đường thẳng trong không gian Toán 12 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12 trang 44.

Giải Toán 12 trang 44 Tập 2 Chân trời sáng tạo

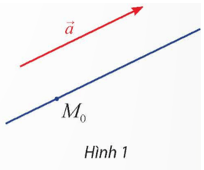
Hoạt động khám phá 1 trang 44 Toán 12 Tập 2: Trong không gian Oxyz, cho điểm M₀ cố định và vectơ $\overrightarrow{a}$ khác $\overrightarrow{0}$. Có bao nhiêu đường thẳng d đi qua M₀ và song song hoặc trùng với giá của $\overrightarrow{a}$.

Lời giải:

Có một đường thẳng d đi qua M₀ và song song hoặc trùng với giá của $\overrightarrow{a}$.

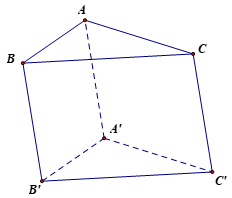
Thực hành 1 trang 44 Toán 12 Tập 2: Trong không gian Oxyz, cho hình lăng trụ tam giác ABC.A'B'C' với A(1; 2; 1), B(7; 5; 3), C(4; 2; 0), A'(4; 9; 9). Tìm tọa độ một vectơ chỉ phương của mỗi đường thẳng AB, A'C' và BB'.

Lời giải:

Ta có $\overrightarrow{AB}=\left(6;3;2\right)$ là một vectơ chỉ phương của đường thẳng AB.

$\overrightarrow{A{A}^{\text{'}}}=\left(3;7;8\right)$ là một vectơ chỉ phương của đường thẳng BB' vì AA' // BB'.

$\overrightarrow{AC}=\left(3;0;-1\right)$ là một vectơ chỉ phương của đường thẳng A'C' vì AC // A'C'.

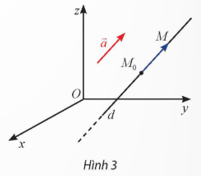
Hoạt động khám phá 2 trang 44 Toán 12 Tập 2: Trong không gian Oxyz, cho đường thẳng d đi qua điểm M₀(x₀; y₀; z₀) cố định và có vectơ chỉ phương là $\overrightarrow{a}=\left(a_1;a_2;a_3\right)$ khác $\overrightarrow{0}$.

a) Giải thích tại sao ta có thể viết: M ∈ d ⇔ $\overrightarrow{M_{0}M}=t\overrightarrow{a},\left(t\in ℝ\right)$

b) Với M(x; y; z) thuộc d, hãy tính x, y, z theo x₀, y₀, z₀ và a₁, a₂, a₃.

Lời giải:

a) Ta có M ∈ d thì $\overrightarrow{M_{0}M}$ cùng phương với $\overrightarrow{a}$. Do đó $\overrightarrow{M_{0}M}=t\overrightarrow{a},\left(t\in ℝ\right)$.

b) Ta có $\overrightarrow{M_{0}M}=\left(x-x_0;y-y_0;z-z_0\right)$.

Mà $\overrightarrow{M_{0}M}=t\overrightarrow{a}$ nên $\left\{\begin{array}{l}x-x_0=a_{1}t\\ y-y_0=a_{2}t\\ z-z_0=a_{3}t\end{array}\right.$$\Rightarrow \left\{\begin{array}{l}x=x_0+a_{1}t\\ y=y_0+a_{2}t\\ z=z_0+a_{3}t\end{array}\right.,t\in ℝ$.

Lời giải bài tập Toán 12 Bài 2: Phương trình đường thẳng trong không gian hay khác:

• Giải Toán 12 trang 46
• Giải Toán 12 trang 47
• Giải Toán 12 trang 49
• Giải Toán 12 trang 52
• Giải Toán 12 trang 53
• Giải Toán 12 trang 55
• Giải Toán 12 trang 56
• Giải Toán 12 trang 59
• Giải Toán 12 trang 60