Giải Toán 12 trang 55 Tập 2 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm lời giải bài tập Toán 12 trang 55 Tập 2 trong Bài 2: Phương trình đường thẳng trong không gian Toán 12 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12 trang 55.

Giải Toán 12 trang 55 Tập 2 Chân trời sáng tạo

Thực hành 9 trang 55 Toán 12 Tập 2: Tính góc giữa hai đường thẳng d và d' trong mỗi trường hợp sau:

a) $d:\frac{x-7}{3}=\frac{y}{5}=\frac{z-11}{4}$ và $d^{\text{'}}:\frac{x-3}{2}=\frac{y+6}{5}=\frac{z-1}{-4}$;

b) $d:\frac{x+9}{3}=\frac{y+4}{6}=\frac{z+1}{6}$ và $d^{\text{'}}:\left\{\begin{array}{l}x=9-10t\\ y=7-10t\\ z=15+5t\end{array}\right.$;

c) $d:\left\{\begin{array}{l}x=23+2t\\ y=57+t\\ z=19-5t\end{array}\right.$ và $d^{\text{'}}:\left\{\begin{array}{l}x=24+t^{\text{'}}\\ y=6+t^{\text{'}}\\ z=t^{\text{'}}\end{array}\right.$.

Lời giải:

a) Đường thẳng d và d' có vectơ chỉ phương lần lượt là $\overrightarrow{a}=\left(3;5;4\right),\overrightarrow{a^{\text{'}}}=\left(2;5;-4\right)$.

Ta có $\cos \left(d,d^{\text{'}}\right)=\frac{\left|3.2+5.5+4.\left(-4\right)\right|}{\sqrt{3^2+5^2+4^2}.\sqrt{2^2+5^2+{\left(-4\right)}^2}}=\frac{15}{15\sqrt{10}}=\frac{1}{\sqrt{10}}$.

Suy ra (d, d') ≈ 71,57°.

b) Đường thẳng d và d' có vectơ chỉ phương lần lượt là $\overrightarrow{a}=\left(3;6;6\right),\overrightarrow{a^{\text{'}}}=\left(-10;-10;5\right)$.

Ta có $\cos \left(d,d^{\text{'}}\right)=\frac{\left|3.\left(-10\right)+6.\left(-10\right)+6.5\right|}{\sqrt{3^2+6^2+6^2}.\sqrt{{\left(-10\right)}^2+{\left(-10\right)}^2+5^2}}=\frac{60}{135}=\frac{4}{9}$.

Suy ra (d, d') ≈ 63,61°.

c) Đường thẳng d và d' có vectơ chỉ phương lần lượt là $\overrightarrow{a}=\left(2;1;-5\right),\overrightarrow{a^{\text{'}}}=\left(1;1;1\right)$

Ta có $\cos \left(d,d^{\text{'}}\right)=\frac{\left|2.1+1.1+\left(-5\right).1\right|}{\sqrt{2^2+1^2+{\left(-5\right)}^2}.\sqrt{1^2+1^2+1^2}}=\frac{2}{3\sqrt{10}}$.

Suy ra (d, d') ≈ 77,83°.

Vận dụng 5 trang 55 Toán 12 Tập 2: Trên một phần mềm đã thiết kế sân khấu 3D trong không gian Oxyz. Tính góc giữa hai tia sáng có phương trình lần lượt là: $d:\frac{x}{2}=\frac{y}{1}=\frac{z}{-1}$ và $d^{\text{'}}:\frac{x-1}{3}=\frac{y-1}{3}=\frac{z-1}{9}$.

Lời giải:

Đường thẳng d và d' có vectơ chỉ phương lần lượt là $\overrightarrow{a}=\left(2;1;-1\right),\overrightarrow{a^{\text{'}}}=\left(3;3;9\right)$

Ta có $\cos \left(d,d^{\text{'}}\right)=\frac{\left|2.3+1.3+\left(-1\right).9\right|}{\sqrt{2^2+1^2+1^2}.\sqrt{3^2+3^2+9^2}}=\frac{0}{3\sqrt{66}}=0$

Suy ra (d, d') = 90°.

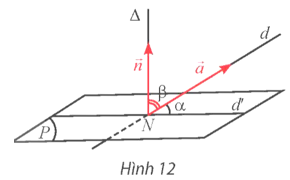
Hoạt động khám phá 9 trang 55 Toán 12 Tập 2: Cho đường thẳng d có vectơ chỉ phương $\overrightarrow{a}=\left(a_1;a_2;a_3\right)$ và mặt phẳng (P) có vectơ pháp tuyến $\overrightarrow{n}=\left(n_1;n_2;n_3\right)$. Biết d cắt (P) tại điểm N và hình chiếu vuông góc của d lên (P) là đường thẳng d'. Qua N vẽ đường thẳng ∆ vuông góc với (P) (Hình 12).

a) Nhắc lại định nghĩa góc giữa đường thẳng và mặt phẳng trong không gian.

b) Có nhận xét gì về số đo của hai góc α = (d, d'); β = (∆, d)?

c) Giải thích tại sao ta lại có đẳng thức: $\sin \left(d,\left(P\right)\right)=\left|\cos \left(\overrightarrow{a},\overrightarrow{n}\right)\right|$

Lời giải:

a) Nếu đường thẳng a không vuông góc với (P) thì góc giữa a và hình chiếu a' của a trên (P) gọi là góc giữa đường thẳng a và (P). Kí hiệu (a, (P)).

b) Ta có α + β = 90° hay (d, d') + (∆, d) = 90° => (d, d') = 90° − (∆, d).

c) Vì (d, (P)) = (d, d') = 90° − (∆, d).

Do đó sin(d, (P)) = sin(90° − (∆, d)) = cos(∆, d) = $\left|\cos \left(\overrightarrow{a},\overrightarrow{n}\right)\right|$

Lời giải bài tập Toán 12 Bài 2: Phương trình đường thẳng trong không gian hay khác:

• Giải Toán 12 trang 44
• Giải Toán 12 trang 46
• Giải Toán 12 trang 47
• Giải Toán 12 trang 49

• Giải Toán 12 trang 52
• Giải Toán 12 trang 53
• Giải Toán 12 trang 56
• Giải Toán 12 trang 59
• Giải Toán 12 trang 60