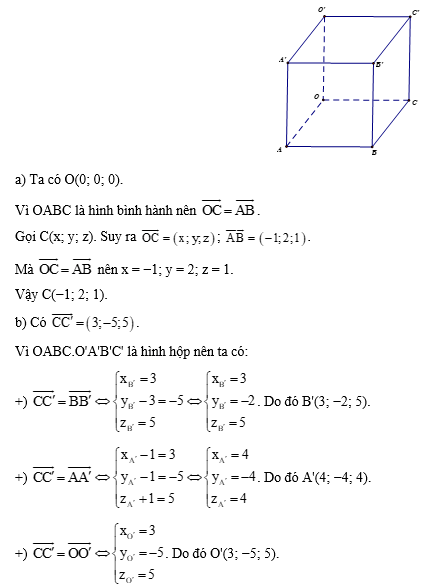Giải Toán 12 trang 65 Tập 1 Kết nối tri thức
Với Giải Toán 12 trang 65 Tập 1 trong Bài 7: Hệ trục toạ độ trong không gian Toán 12 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12 trang 65.
Giải Toán 12 trang 65 Tập 1 Kết nối tri thức
Bài 2.15 trang 65 Toán 12 Tập 1: Trong không gian Oxyz, xác định tọa độ của vectơ trong mỗi trường hợp sau:
a) A(0; 0; 0) và B(4; 2; −5);
b) A(1; −3; 7) và B(1; −3; 7);
c) A(5; 4; 9) và B(−5; 7; 2).
Lời giải:
a) .
b) .
c) .
Bài 2.16 trang 65 Toán 12 Tập 1: Trong không gian Oxyz, xác định tọa độ của điểm A trong mỗi trường hợp sau:
a) A trùng với gốc tọa độ;
b) A nằm trên tia Ox và OA = 2.
c) A nằm trên tia đối của tia Oy và OA = 3.
Lời giải:
a) A(0; 0; 0).
b) A nằm trên tia Ox và OA = 2 nên . Suy ra A(2; 0; 0).
c) A nằm trên tia đối của tia Oy và OA = 3 nên . Suy ra A(0; −3; 0).
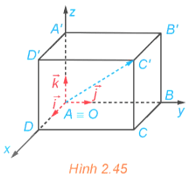
Bài 2.17 trang 65 Toán 12 Tập 1: Trong không gian Oxyz, cho hình hộp chữ nhật ABCD.A'B'C'D' có đỉnh A trùng với gốc O và các đỉnh D, B, A' có tọa độ lần lượt là (2; 0; 0), (0; 4; 0), (0; 0; 3) (H.2.45). Xác định tọa độ của các đỉnh còn lại của hình hộp chữ nhật.
Lời giải:
Đỉnh A trùng với gốc tọa độ nên A(0; 0; 0).
Ta có D(2; 0; 0) nên ; B(0; 4; 0) nên ; A'(0; 0; 3) nên .
Theo quy tắc hình hộp, ta có: .
Do đó C'(2; 4; 3).
Theo quy tắc hình bình hành, ta có: .
Do đó C(2; 4; 0).
Theo quy tắc hình bình hành, ta có: .
Do đó D'(2; 0; 3).
Theo quy tắc hình bình hành, ta có: .
Do đó B'(0; 4; 3).
Bài 2.18 trang 65 Toán 12 Tập 1: Trong không gian Oxyz, cho hình hộp OABC.O'A'B'C' có A(1; 1; −1), B(0; 3; 0), C'(2; −3; 6).
a) Xác định tọa độ của điểm C.
b) Xác định tọa độ các đỉnh còn lại của hình hộp.
Lời giải:
Bài 2.19 trang 65 Toán 12 Tập 1: Trong Vận dụng 2, hãy giải thích vì sao tại mỗi thời điểm chiếc máy bay di chuyển trên đường băng thì tọa độ của nó luôn có dạng (x; y; 0) với x, y là hai số thực nào đó.
Lời giải:
Khi máy bay di chuyển trên đường băng tức là máy bay di chuyển ở trên mặt đất,tức là thuộc mặt phẳng (Oxy). Do đó máy bay khi di chuyển trên đường băng thì tọa độ của nó luôn có dạng (x; y; 0) với x, y là hai số thực nào đó.
Lời giải bài tập Toán 12 Bài 7: Hệ trục toạ độ trong không gian hay khác: