Bài 6 trang 92 Toán 7 Tập 2 Cánh diều

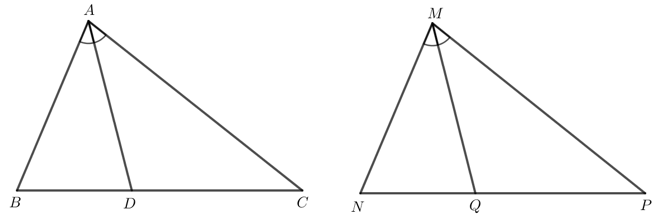
Cho ∆ABC = ∆MNP. Tia phân giác của góc BAC và MP lần lượt cắt các cạnh BC và NP tại D, Q. Chứng minh AD = MQ.

Giải Toán 7 Bài 6: Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc - Cánh diều

Bài 6 trang 92 Toán lớp 7 Tập 2: Cho ∆ABC = ∆MNP. Tia phân giác của góc BAC và NMP lần lượt cắt các cạnh BC và NP tại D, Q. Chứng minh AD = MQ.

Lời giải:

Do ∆ABC = ∆MNP nên $\hat{B A C} = \hat{N M P}$ (2 góc tương ứng), $\hat{A C B} = \hat{M P N}$ (2 góc tương ứng) và AC = MP (2 cạnh tương ứng).

Do AD là tia phân giác của $\hat{B A C}$ nên $\hat{D A C} = \frac{1}{2} \hat{B A C}$ .

Do MQ là tia phân giác của $\hat{N M P}$ nên $\hat{Q M P} = \frac{1}{2} \hat{N M P}$ .

Mà $\hat{B A C} = \hat{N M P}$ nên $\hat{D A C} = \hat{Q M P}$ .

Xét ∆ADC và ∆MQP có:

$\hat{D A C} = \hat{Q M P}$ (chứng minh trên).

AC = MP (chứng minh trên).

$\hat{A C D} = \hat{M P Q}$ (chứng minh trên).

Suy ra ∆ADC = ∆MQP (g - c - g).

Do đó AD = MQ (2 cạnh tương ứng).

Lời giải bài tập Toán 7 Bài 6: Trường hợp bằng nhau thứ ba của tam giác: góc - cạnh - góc hay, chi tiết khác: