Kiểm tra lại bằng thước đo góc để thấy các góc xOC và yOC trong
Câu hỏi:
Kiểm tra lại bằng thước đo góc để thấy các góc xOC và yOC trong Hoạt động 2 là bằng nhau.
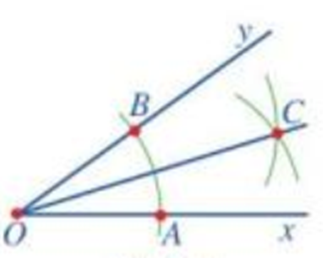
Trả lời:
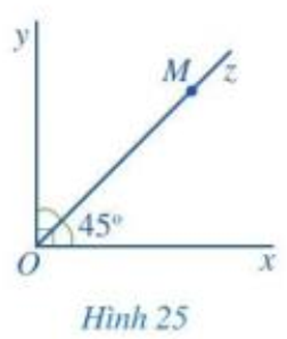
Từ Hoạt động 2, ta thu được hình vẽ như sau:
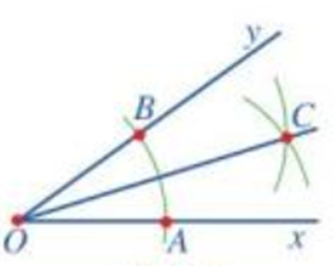
Dùng thước đo góc, đo số đo các góc xOC và góc yOC, ta được:
; .
Do đó, .