Giải Toán 7 trang 61 Tập 2 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm với giải Toán 7 trang 61 Tập 2 trong Bài 3: Tam giác cân Toán lớp 7 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 7 trang 61.

Giải Toán 7 trang 61 Tập 2 Chân trời sáng tạo

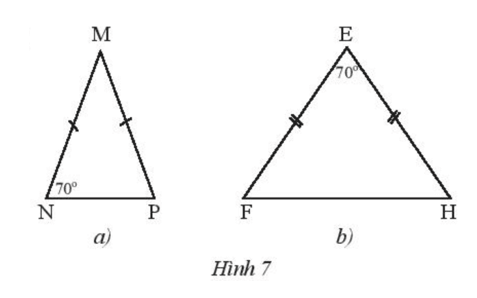
Thực hành 2 trang 61 Toán 7 Tập 2: Tìm số đo các góc chưa biết của mỗi tam giác trong Hình 7.

Lời giải:

Tam giác MNP có MN = MP nên tam giác MNP cân tại M.

Do đó $\widehat{MNP}=\widehat{MPN}=70°$.

Trong tam giác MNP: $\widehat{NMP}=180°-\widehat{MNP}-\widehat{MPN}=180°-70°-70°=40°$.

Tam giác EFH có EF = EH nên tam giác EFH cân tại E.

Do đó $\widehat{EFH}=\widehat{EHF}$.

Trong tam giác EFH: $\widehat{F\text{E}H}+\widehat{EFH}+\widehat{EHF}=180°$.

Suy ra $2\widehat{EFH}=180°-\widehat{FEH}=180°-70°=110°$.

Do đó $\widehat{EFH}=\widehat{EHF}=55°$.

Vậy $\hat{M}$= 40°; $\hat{P}$= 70°; $\hat{F}=\hat{H}$= 55°.

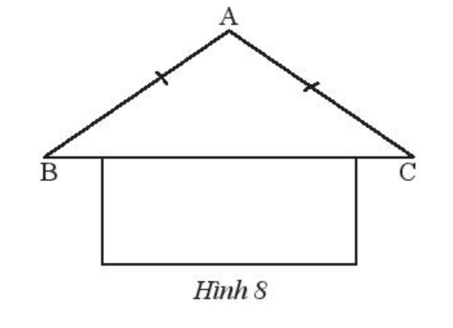
Vận dụng 1 trang 61 Toán 7 Tập 2: Trong hình mái nhà ở Hình 8, tính góc B và góc C, biết $\hat{A}=110°$.

Lời giải:

Tam giác ABC có AB = AC nên tam giác ABC cân tại A.

Do đó $\hat{B}=\hat{C}$.

Trong tam giác ABC: $\hat{A}+\hat{B}+\hat{C}=180°$.

Suy ra $2\hat{B}=180°-\hat{A}=180°-110°=70°$.

Do đó $\hat{B}=\hat{C}=35°$.

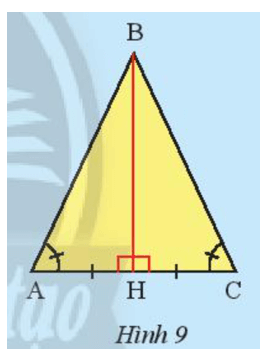
Khám phá 3 trang 61 Toán 7 Tập 2: Cho tam giác ABC có $\hat{A}=\hat{C}$. Vẽ đường thẳng đi qua điểm B, vuông góc với AC và cắt AC tại điểm H (Hình 9). Em hãy làm theo gợi ý sau để chứng minh BA = BC.

Xét $\Delta AHB$và $\Delta CHB$cùng vuông tại H, ta có:

BH là cạnh góc vuông ?;

$\widehat{HAB}=\widehat{HCB}$suy ra $\widehat{ABH}=\widehat{CBH}$(?).

Vậy $△$AHB = $△$CHB. Suy ra BA = BC.

Lời giải:

Xét $\Delta AHB$và $\Delta CHB$cùng vuông tại H, ta có:

BH là cạnh góc vuông chung;

$\widehat{HAB}=\widehat{HCB}$suy ra $\widehat{ABH}=\widehat{CBH}$(do $\widehat{ABH}=90°-\widehat{HAB}$và $\widehat{CBH}=90°-\widehat{HCB}$).

Vậy $\Delta AHB=\Delta CHB$. Suy ra BA = BC.

Lời giải bài tập Toán lớp 7 Bài 3: Tam giác cân Chân trời sáng tạo hay khác:

• Giải Toán 7 trang 59 Tập 2

• Giải Toán 7 trang 60 Tập 2

• Giải Toán 7 trang 62 Tập 2

• Giải Toán 7 trang 63 Tập 2