Giải Toán 7 trang 63 Tập 2 Chân trời sáng tạo

❮ Bài trước Bài sau ❯

Haylamdo biên soạn và sưu tầm với giải Toán 7 trang 63 Tập 2 trong Bài 3: Tam giác cân Toán lớp 7 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 7 trang 63.

Giải Toán 7 trang 63 Tập 2 Chân trời sáng tạo

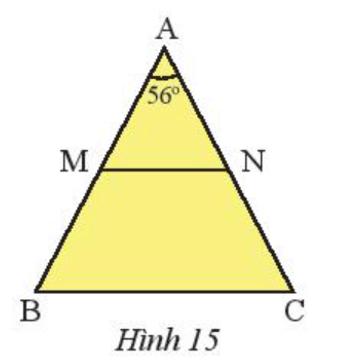
Bài 3 trang 63 Toán 7 Tập 2: Cho tam giác ABC cân tại A có $\hat{A} = 56 °$ (Hình 15).

Cho tam giác ABC cân tại A có góc A = 56 độ

a) Tính $\hat{B}, \hat{C}$ .

b) Gọi M, N lần lượt là trung điểm của AB, AC. Chứng minh rằng tam giác AMN cân.

c) Chứng minh rằng MN // BC.

Lời giải:

a) Tam giác ABC cân tại A nên $\hat{A B C} = \hat{A C B}$ .

Trong tam giác ABC có: $\hat{A B C} + \hat{A C B} = 180 ° - \hat{B A C}$ .

Do đó $2 \hat{A B C} = 180 ° - 56 ° = 124 °$ .

Suy ra $\hat{A B C} = \hat{A C B} = 62 °$ .

b) Do M là trung điểm của AB nên AM = $\frac{1}{2}$ AB.

Do N là trung điểm của AC nên AN = $\frac{1}{2}$ AC.

Do tam giác ABC cân tại A nên AB = AC.

Do đó AM = AN.

Tam giác AMN có AM = AN nên tam giác AMN cân tại A.

c) Do tam giác AMN cân tại A nên $\hat{A M N} = \hat{A N M}$ .

Trong tam giác AMN có: $\hat{A M N} + \hat{A N M} = 180 ° - \hat{N A M}$ .

Do đó $2 \hat{A M N} = 180 ° - 56 ° = 124 °$ .

Suy ra $\hat{A M N} = \hat{A N M} = 62 °$ .

Khi đó $\hat{A B C} = \hat{A M N} = 62 °$ .

Mà hai góc này ở vị trí đồng vị nên MN // BC.

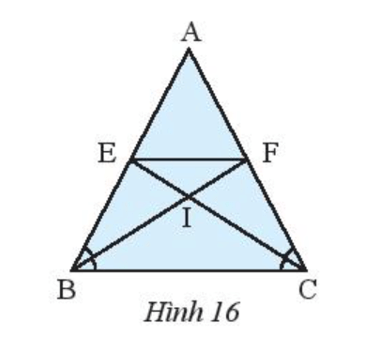
Bài 4 trang 63 Toán 7 Tập 2: Cho tam giác ABC cân tại A (Hình 16). Tia phân giác của góc B cắt AC tại F, tia phân giác của góc C cắt AB tại E.

Cho tam giác ABC cân tại A (Hình 16). Tia phân giác của góc B cắt AC tại F

a) Chứng minh rằng $\hat{A B F} = \hat{A C E}$ .

b) Chứng minh rằng tam giác AEF cân.

c) Gọi I là giao điểm của BF và CE. Chứng minh rằng tam giác IBC và tam giác IEF là những tam giác cân.

Lời giải:

a) Do tam giác ABC cân tại A nên AB = AC và $\hat{A B C} = \hat{A C B}$ .

Do BF là tia phân giác của $\hat{A B C}$ nên $\hat{A B F} = \hat{F B C} = \frac{1}{2} \hat{A B C}$ .

Do CE là tia phân giác của $\hat{A C B}$ nên $\hat{A C E} = \hat{E C B} = \frac{1}{2} \hat{A C B}$ .

Do đó $\hat{A B F} = \hat{A C E}$ .

b) Xét $Δ A B F$ và $Δ A C E$ có:

$\hat{A B F} = \hat{A C E}$ (chứng minh trên).

AB = AC (chứng minh trên).

$\hat{A}$ chung.

Do đó $Δ A B F = Δ A C E$ (g.c.g).

Suy ra AF = AE (2 cạnh tương ứng).

Tam giác AEF có AF = AE nên tam giác AEF cân tại A.

c) Ta có $\hat{F B C} = \hat{E C B}$ nên $\hat{I B C} = \hat{I C B}$ .

Tam giác IBC có $\hat{I B C} = \hat{I C B}$ nên tam giác IBC cân tại I.

Do đó IB = IC.

Xét $Δ E I B$ và $Δ F I C$ có:

$\hat{E I B} = \hat{F I C}$ (đối đỉnh).

IB = IC (chứng minh trên).

$\hat{E B I} = \hat{F C I}$ (chứng minh trên).

Do đó $Δ E I B = Δ F I C$ (g.c.g).

Suy ra IE = IF (2 cạnh tương ứng).

Tam giác IEF có IE = IF nên tam giác IEF cân tại I.

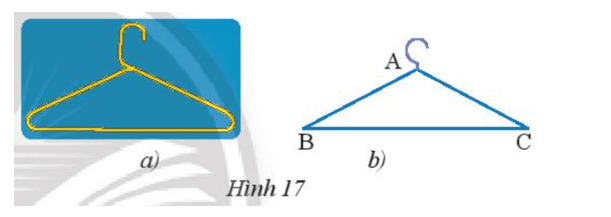
Bài 5 trang 63 Toán 7 Tập 2: Phần thân của một móc treo quần áo có dạng hình tam giác cân (Hình 17a) được vẽ lại như Hình 17b. Cho biết AB = 20 cm; BC = 28 cm và $\hat{B} = 35 °$ . Tìm số đo các góc còn lại và chu vi của tam giác ABC.

Phần thân của một móc treo quần áo có dạng hình tam giác cân

Lời giải:

Dựa vào Hình 17b và tam giác ABC cân nên tam giác ABC cân tại A.

Do đó AB = AC và $\hat{B} = \hat{C}$ .

Khi đó AC = 20 cm và $\hat{C} = 35 °$ .

Chu vi của DABC bằng: 20 + 20 + 28 = 68 (cm).

Trong tam giác ABC có: $\hat{A} = 180 ° - \hat{B} - \hat{C} = 180 ° - 35 ° - 35 ° = 110 °$ .

Vậy $\hat{A} = 110 °$ ; $\hat{C} = 35 °$ ; chu vi của tam giác ABC bằng 68 cm.

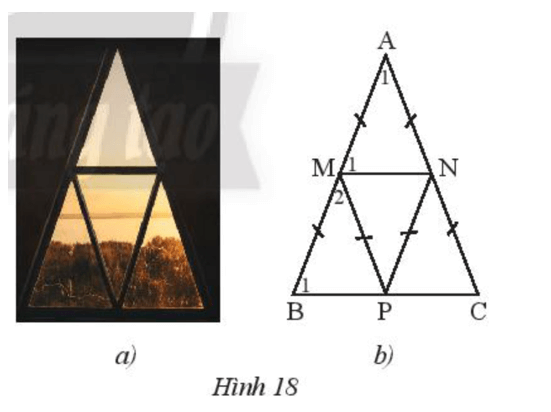
Bài 6 trang 63 Toán 7 Tập 2: Một khung cửa sổ hình tam giác có thiết kế như Hình 18a được vẽ lại như Hình 18b.

Một khung cửa sổ hình tam giác có thiết kế như Hình 18a được vẽ lại như Hình 18b

a) Cho biết ${\hat{A}}_{1} = 42 °$ . Tính số đo của ${\hat{M}}_{1}, {\hat{B}}_{1}, {\hat{M}}_{2}$ .

b) Chứng minh MN // BC, MP // AC.

c) Chứng minh bốn tam giác cân AMN, MBP, PMN, NPC bằng nhau.

Lời giải:

a) $Δ A M N$ có AM = AN nên $Δ A M N$ cân tại A.

Khi đó $\hat{A M N} = \hat{A N M}$ .

Trong tam giác AMN có: $\hat{A M N} + \hat{A N M} = 180 ° - \hat{M A N}$ .

Hay $2 {\hat{M}}_{1} = 180 ° - {\hat{A}}_{1} = 180 ° - 42 ° = 138 °$ .

Do đó ${\hat{M}}_{1} = 69 °$ .

Tam giác ABC có AB = AM + MB, AC = AN + NC.

Mà AM = AN, MB = NC nên AB = AC.

Do đó $Δ A B C$ cân tại A.

Khi đó $\hat{A B C} = \hat{A C B}$ .

Trong tam giác ABC có: $\hat{A B C} + \hat{A C B} = 180 ° - \hat{B A C}$ .

Hay $2 {\hat{B}}_{1} = 180 ° - {\hat{A}}_{1} = 180 ° - 42 ° = 138 °$ .

Do đó ${\hat{B}}_{1} = 69 °$ .

Tam giác MBP có MB = MP nên tam giác MBP cân tại M.

Do đó $\hat{M B P} = \hat{M P B}$ .

Trong tam giác MBP có: $\hat{B M P} = 180 ° - \hat{M B P} - \hat{M P B}$ .

Hay ${\hat{M}}_{2} = 180 ° - 2 {\hat{B}}_{1} = 180 ° - 2.69 ° = 42 °$ .

Vậy ${\hat{M}}_{1} = 69 °$ ; ${\hat{B}}_{1} = 69 °$ ; ${\hat{M}}_{2} = 42 °$ .

b) Ta có ${\hat{M}}_{1} = {\hat{B}}_{1} = 69 °$ , mà hai góc này ở vị trí đồng vị nên MN // BC.

${\hat{M}}_{2} = {\hat{A}}_{1} = 42 °$ , mà hai góc này ở vị trí đồng vị nên MP // AC.

c) Xét $Δ A M N$ và $Δ M B P$ có:

AM = MB (theo giả thiết).

$\hat{M A N} = \hat{B M P}$ (chứng minh trên).

AN = MP (theo giả thiết).

Do đó $Δ A M N = Δ M B P$ (c.g.c).

Suy ra MN = BP (2 cạnh tương ứng).

Xét $Δ M B P$ và $Δ P M N$ có:

MB = PM (theo giả thiết).

BP = MN (chứng minh trên).

MP = PN (theo giả thiết).

Do đó $Δ M B P = Δ P M N$ (c.c.c).

Do MP // AC nên $\hat{M P N} = \hat{P N C}$ (2 góc so le trong).

Xét $Δ P M N$ và $Δ N P C$ có:

PM = NP (theo giả thiết).

$\hat{M P N} = \hat{P N C}$ (chứng minh trên).

PN = NC (theo giả thiết).

Do đó $Δ P M N = Δ N P C$ (c.g.c).

Vậy bốn tam giác cân AMN, MBP, PMN, NPC bằng nhau.

Lời giải bài tập Toán lớp 7 Bài 3: Tam giác cân Chân trời sáng tạo hay khác:

Xem thêm lời giải bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:

❮ Bài trước Bài sau ❯

Giải Toán lớp 7 Chân trời sáng tạo

Giải Toán 7 trang 63 Tập 2 Chân trời sáng tạo

Giải Toán 7 trang 63 Tập 2 Chân trời sáng tạo

Xem thêm lời giải bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác: