Giải Toán 7 trang 62 Tập 2 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm với giải Toán 7 trang 62 Tập 2 trong Bài 3: Tam giác cân Toán lớp 7 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 7 trang 62.

Giải Toán 7 trang 62 Tập 2 Chân trời sáng tạo

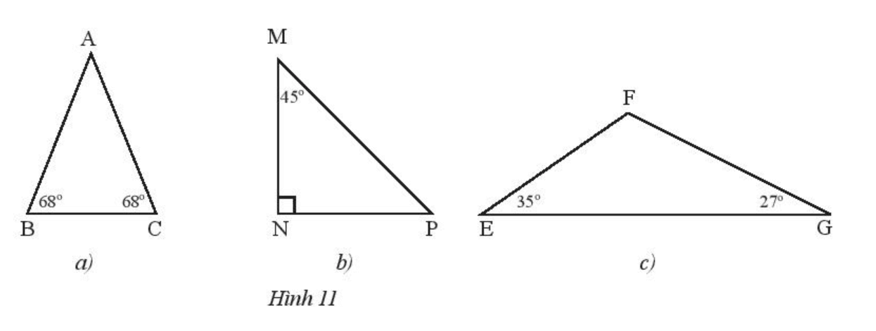
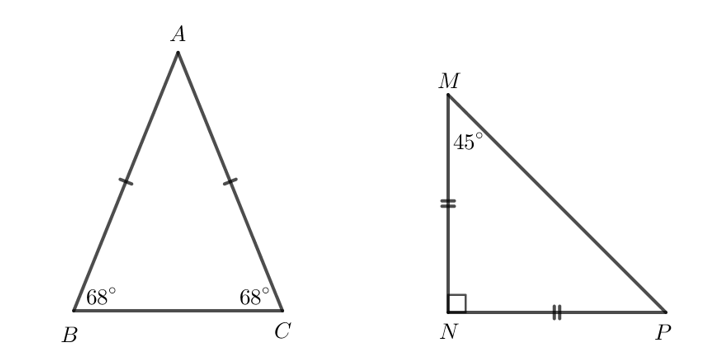
Thực hành 3 trang 62 Toán 7 Tập 2: Tìm các tam giác cân trong Hình 11 và đánh dấu các cạnh bằng nhau.

Lời giải:

Tam giác ABC có $\widehat{ABC}=\widehat{ACB}=68°$nên tam giác ABC cân tại A.

Do đó AB = AC.

Tam giác MNP vuông tại N nên $\widehat{NPM}=90°-\widehat{NMP}=90°-45°=45°$(trong tam giác vuông, tổng hai góc nhọn bằng $90°$).

Tam giác MNP có $\widehat{NMP}=\widehat{NPM}=45°$nên tam giác MNP cân tại N.

Do đó NM = NP.

Tam giác EFG có $\hat{E}=35°$, $\hat{G}=27°$, $\hat{F}$là góc tù nên tam giác EFG không có hai góc nào bằng nhau.

Do đó tam giác EFG không phải tam giác cân.

Ta có hình vẽ sau:

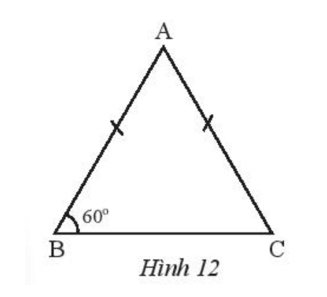
Vận dụng 2 trang 62 Toán 7 Tập 2: Cho tam giác ABC cân tại A có góc B bằng 60°.

Chứng minh rằng tam giác ABC đều.

Lời giải:

Tam giác ABC cân tại A nên AB = AC và $\hat{B}=\hat{C}=60°$.

Tam giác ABC có: $\hat{A}=180°-\hat{B}-\hat{C}=180°-60°-60°=60°$.

Tam giác ABC có $\hat{B}=\hat{A}$nên tam giác ABC cân tại C.

Do đó CA = CB.

Mà AB = AC nên AB = AC = BC.

Vậy tam giác ABC là tam giác đều.

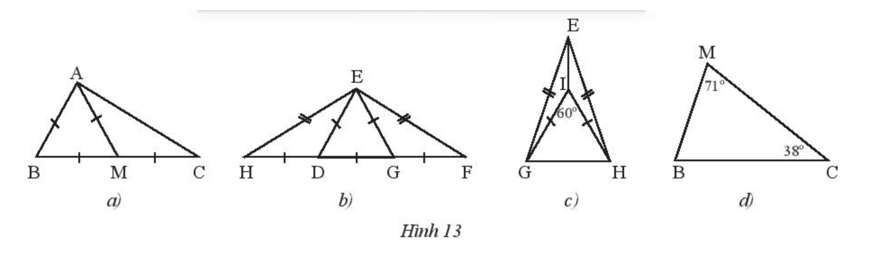
Bài 1 trang 62 Toán 7 Tập 2: Tìm các tam giác cân và tam giác đều trong mỗi hình sau (Hình 13). Giải thích.

Lời giải:

+) Xét Hình 13a:

$\Delta AMC$có AM = MC nên $\Delta AMC$cân tại M.

$\Delta ABM$có AB = AM = BM nên $\Delta ABM$đều.

+) Xét Hình 13b:

$\Delta DEH$có DE = DH nên $\Delta DEH$cân tại D.

$\Delta GEF$có GE = GF nên $\Delta GEF$cân tại G.

$\Delta EHF$có EH = EF nên $\Delta EHF$cân tại E.

Do đó các tam giác cân: $\Delta DEH$, $\Delta GEF$, $\Delta EHF$.

$\Delta E\text{D}G$có DE = EG = DG nên $\Delta E\text{D}G$đều.

+) Xét Hình 13c:

$\Delta EGH$có EG = EH nên $\Delta EGH$cân tại E.

$\Delta IGH$có IG = IH nên $\Delta IGH$cân tại I.

$\Delta IGH$cân có $\widehat{GIH}=60°$nên $\Delta IGH$đều.

+) Xét Hình 13d:

Trong tam giác MBC có: $\hat{B}=180°-\hat{M}-\hat{C}=180°-71°-38°=71°$.

Tam giác MBC có $\hat{M}=\hat{B}$nên tam giác MBC cân tại C.

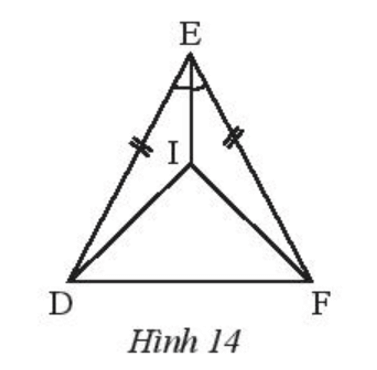
Bài 2 trang 62 Toán 7 Tập 2: Cho Hình 14, biết ED = EF và EI là tia phân giác của $\widehat{DEF}$.

Chứng minh rằng:

a) $\Delta EI\text{D}=\Delta E\text{IF}$.

b) Tam giác DIF cân.

Lời giải:

a) Do EI là tia phân giác của $\widehat{DEF}$nên $\widehat{DEI}=\widehat{F\text{E}I}$.

Xét $\Delta EI\text{D}$và $\Delta EIF$có:

ED = EF (theo giả thiết).

$\widehat{DEI}=\widehat{F\text{E}I}$(chứng minh trên).

EI chung.

Do đó $\Delta EI\text{D}=\Delta EIF$(c.g.c).

b) Do $\Delta EI\text{D}=\Delta EIF$(c.g.c) nên ID = IF (2 cạnh tương ứng).

Tam giác DIF có ID = IF nên tam giác DIF cân tại I.

Lời giải bài tập Toán lớp 7 Bài 3: Tam giác cân Chân trời sáng tạo hay khác:

• Giải Toán 7 trang 59 Tập 2

• Giải Toán 7 trang 60 Tập 2

• Giải Toán 7 trang 61 Tập 2

• Giải Toán 7 trang 63 Tập 2