Bài 9.24 trang 76 Toán 7 Tập 2 - Kết nối tri thức
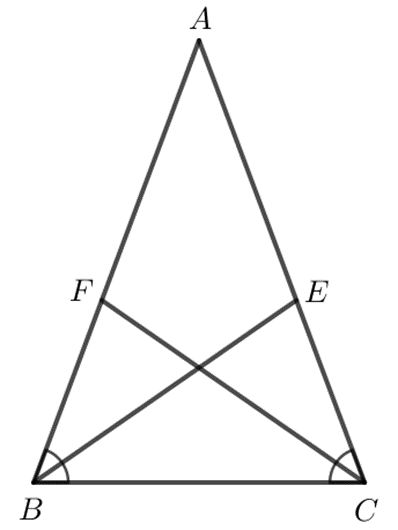
Gọi BE và CF là hai đường phân giác của tam giác ABC cân tại A. Chứng minh BE = CF.
Giải Toán 7 Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác
Bài 9.24 trang 76 Toán 7 Tập 2: Gọi BE và CF là hai đường phân giác của tam giác ABC cân tại A. Chứng minh BE = CF.
Lời giải:
Do ∆ABC cân tại A nên .
Do BE là tia phân giác của nên .
Do CF là tia phân giác của nên .
Mà nên .
Xét ∆FBC và ∆ECB có:
(chứng minh trên).
BC chung.
(chứng minh trên).
Suy ra ∆FBC = ∆ECB (g - c - g).
Do đó CF = BE (2 cạnh tương ứng).
Vậy BE = CF.
Lời giải bài tập Toán 7 Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác hay, chi tiết khác: