Vận dụng 2 trang 75 Toán 7 Tập 2 - Kết nối tri thức

Chứng minh rằng trong tam giác đều, điểm cách đều ba cạnh của tam giác là trọng tâm của tam giác đó.

Giải Toán 7 Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác

Vận dụng 2 trang 75 Toán 7 Tập 2: Chứng minh rằng trong tam giác đều, điểm cách đều ba cạnh của tam giác là trọng tâm của tam giác đó.

Lời giải:

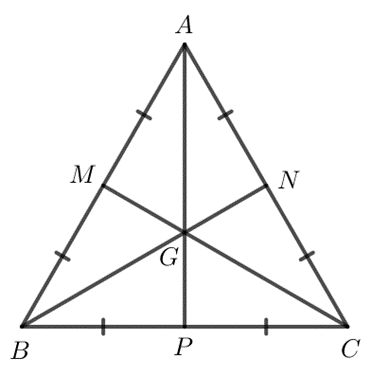
Vận dụng 2 trang 75 Toán 7 Tập 2 | Kết nối tri thức Giải Toán lớp 7

Giả sử tam giác ABC là tam giác đều có M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC và G là trọng tâm của tam giác.

Khi đó A, G, P thẳng hàng; B, G, N thẳng hàng; C, G, M thẳng hàng.

Tam giác ABC đều nên AB = BC = CA và $\hat{A B C} = \hat{B A C} = \hat{A C B}$ .

Xét ∆APB và ∆APC có:

AB = AC (chứng minh trên).

AP chung.

PB = PC (do P là trung điểm của BC).

Suy ra ∆APB = ∆APC (c-c-c).

Do đó $\hat{A P B} = \hat{A P C}$ (2 góc tương ứng).

Mà $\hat{A P B} + \hat{A P C} = 180 °$ nên $\hat{A P B} = \hat{A P C} = 90 °$ do đó AP ⊥ BC hay GP ⊥ BC.

Khi đó GP là khoảng cách từ G đến BC.

Tương tự ta có GM, GN lần lượt là khoảng cách từ G đến AC, AC.

Do M là trung điểm của AB nên MB = $\frac{1}{2}$ AB.

Do N là trung điểm của AC nên NC = $\frac{1}{2}$ AC.

Mà AB = AC nên MB = NC.

Xét ∆MBC và ∆NCB có:

MB = NC (chứng minh trên).

$\hat{M B C} = \hat{N C B}$ (chứng minh trên).

BC chung.

Suy ra ∆MBC = ∆NCB (c-g-c).

Do đó CM = BN (2 cạnh tương ứng).

Tam giác ABC có G là trọng tâm nên CG = $\frac{2}{3}$ CM và BG = $\frac{2}{3}$ BN.

Suy ra GM = $\frac{1}{3}$ CM và GN = $\frac{1}{3}$ BN.

Mà CM = BN nên GM = GN.

Chứng minh tương tự ta có GM = GN = GP.

Khi đó trọng tâm G của tam giác đều ABC cách đều ba cạnh của tam giác.

Vậy trong tam giác đều, điểm cách đều ba cạnh của tam giác là trọng tâm của tam giác đó.

Lời giải bài tập Toán 7 Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác hay, chi tiết khác: