Bài 9.25 trang 76 Toán 7 Tập 2 - Kết nối tri thức
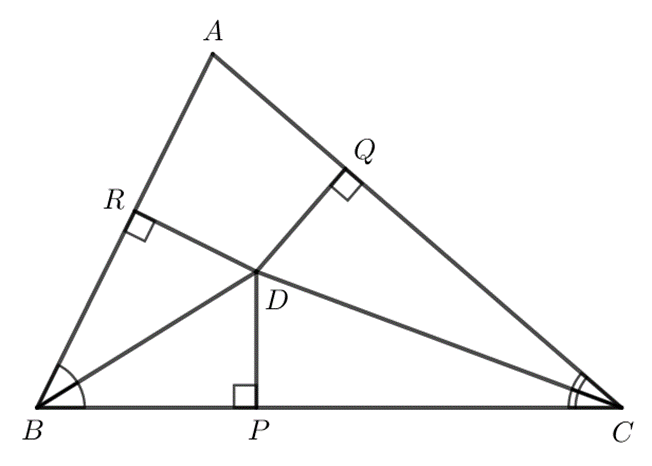
Trong tam giác ABC, hai đường phân giác của các góc B và C cắt nhau tại D. Kẻ DP vuông góc với BC, DQ vuông góc với CA, DR vuông góc với AB.
Giải Toán 7 Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác
Bài 9.25 trang 76 Toán 7 Tập 2: Trong tam giác ABC, hai đường phân giác của các góc B và C cắt nhau tại D. Kẻ DP vuông góc với BC, DQ vuông góc với CA, DR vuông góc với AB.
a) Hãy giải thích tại sao DP = DR.
b) Hãy giải thích tại sao DP = DQ.
c) Từ câu a và b suy ra DR = DQ. Tại sao D nằm trên tia phân giác của góc A?
Lời giải:
a) Do BD là tia phân giác của nên .
Xét ∆DBR vuông tại R và ∆DBP vuông tại P có:
(chứng minh trên).
BD chung.
Suy ra ∆DBR = ∆DBP (cạnh huyền - góc nhọn).
Do đó DR = DP (2 cạnh tương ứng).
b) Do CD là tia phân giác của nên .
Xét ∆DCQ vuông tại Q và ∆DCP vuông tại P có:
(chứng minh trên).
CD chung.
Suy ra ∆DCQ = ∆DCP (cạnh huyền - góc nhọn).
Do đó DQ = DP (2 cạnh tương ứng).
c) Từ ý a và b ta có DR = DP và DQ = DP nên DR = DQ.
Ta có D nằm trong và D cách đều hai cạnh AB và AC của nên D nằm trên tia phân giác của .
Lời giải bài tập Toán 7 Bài 34: Sự đồng quy của ba đường trung tuyến, ba đường phân giác trong một tam giác hay, chi tiết khác: