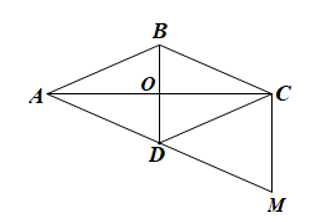
Bài 12 trang 121 Toán 8 Tập 1 Cánh diều

Cho hình thoi ABCD và hình bình hành BCMD. Gọi O là giao điểm của AC và BD. Chứng minh:

Giải Toán 8 Bài tập cuối chương 5 - Cánh diều

Bài 12 trang 121 Toán 8 Tập 1: Cho hình thoi ABCD và hình bình hành BCMD. Gọi O là giao điểm của AC và BD. Chứng minh:

a) $O D = \frac{1}{2} C M$ và tam giác ACM là tam giác vuông;

b) Ba điểm A, D, M thẳng hàng;

c) Tam giác DCM là tam giác cân.

Lời giải:

Bài 12 trang 121 Toán 8 Tập 1 Cánh diều | Giải Toán 8

a) • Do ABCD là hình thoi nên hai đường chéo AC và BD vuông góc với nhau tại trung điểm O của mỗi đường.

Suy ra $O D = \frac{1}{2} B D$ .

Do BCMD là hình bình hành nên BD = CM.

Do đó $O D = \frac{1}{2} C M$ .

• Ta có: CM // BD (do BCMD là hình bình hành)

AC ⊥ BD (chứng minh trên)

Do đó CM ⊥ AC hay $\hat{M C A} = 90 °$

Vây tam giác ACM là tam giác vuông.

b) Vì ABCD là hình thoi nên AD // BC

Vì BCMD là hình bình hành nên DM // BC

Do đó qua điểm D có hai đường thẳng AD và DM cùng song song với đường thẳng BC nên AD trùng với DM (Tiên đề Euclid)

Hay ba điểm A, D, M thẳng hàng.

c) Ta có: BD // CM (chứng minh câu a) nên:

• $\hat{B D C} = \hat{D C M}$ (so le trong); (1)

• $\hat{A D B} = \hat{D M C}$ (đồng vị) (2)

Do ABCD là hình thoi nên DB là tia phân giác của góc ADC

Do đó $\hat{A D B} = \hat{B D C}$ (3)

Từ (1), (2) và (3) suy ra $\hat{D C M} = \hat{D M C}$ .

Xét ΔDCM có $\hat{D C M} = \hat{D M C}$ nên là tam giác cân tại D.

Lời giải bài tập Toán 8 Bài tập cuối chương 5 hay, chi tiết khác: