Bài 9 trang 121 Toán 8 Tập 1 Cánh diều
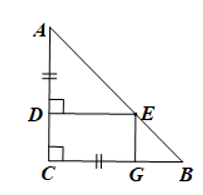
Cho tam giác ABC vuông cân tại C. Trên các cạnh AC, BC lần lượt lấy các điểm D, G sao cho AD = CG < AC. Từ điểm D kẻ DE vuông góc với AC (E thuộc AB). Chứng minh tứ giác CDEG là hình chữ nhật.
Giải Toán 8 Bài tập cuối chương 5 - Cánh diều
Bài 9 trang 121 Toán 8 Tập 1: Cho tam giác ABC vuông cân tại C. Trên các cạnh AC, BC lần lượt lấy các điểm D, G sao cho AD = CG < AC. Từ điểm D kẻ DE vuông góc với AC (E thuộc AB). Chứng minh tứ giác CDEG là hình chữ nhật.
Lời giải:
Vì ΔABC vuông cân tại C (giả thiết) nên .
Xét ΔADE vuông tại D (do DE ⊥ AC) có:
(trong tam giác vuông, tổng hai góc nhọn bằng 90°)
Suy ra
ΔADE vuông tại D có (cùng bằng 45°) nên là tam giác vuông cân tại D
Do đó AD = ED.
Mà AD = CG nên ED = CG.
Xét tứ giác CDEG có:
• ED = CG (chứng minh trên);
• ED // CG (do cùng vuông góc với AC)
Do đó CDEG là hình bình hành
Lại có
Suy ra CDEG là hình chữ nhật.
Lời giải bài tập Toán 8 Bài tập cuối chương 5 hay, chi tiết khác:
Bài 1 trang 120 Toán 8 Tập 1: Cho tứ giác ABCD có . Khi đó, bằng ....
Bài 2 trang 120 Toán 8 Tập 1: Cho hình thang cân ABCD có AB // CD, . Khi đó, bằng ....