Bài 13 trang 121 Toán 8 Tập 1 Cánh diều
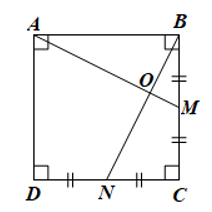
Cho hình vuông ABCD có M, N lần lượt là trung điểm của các cạnh BC, CD. Gọi O là giao điểm của AM và BN. Chứng minh:
Giải Toán 8 Bài tập cuối chương 5 - Cánh diều
Bài 13 trang 121 Toán 8 Tập 1: Cho hình vuông ABCD có M, N lần lượt là trung điểm của các cạnh BC, CD. Gọi O là giao điểm của AM và BN. Chứng minh:
a) ΔABM = ΔBCN;
b) ;
c) AM ⊥ BN.
Lời giải:
a) Do ABCD là hình vuông nên AB = BC = CD = DA.
Vì M là trung điểm của BC nên ;
N là trung điểm của CD nên .
Do đó MB = MC = NC = ND.
Xét ΔABM và ΔBCN có:
(do ABCD là hình vuông);
AB = CD (chứng minh trên);
MB = NC (chứng minh trên)
Do đó ΔABM = ΔBCN (hai cạnh góc vuông).
b) Vì ΔABM = ΔBCN (câu a) nên (hai góc tương ứng).
Hay .
c) Xét ΔABM vuông tại B có
Mà (câu b) nên .
Xét ΔMBO có (tổng ba góc trong một tam giác)
Suy ra .
Do đó OM ⊥ BO hay AM ⊥ BN.
Lời giải bài tập Toán 8 Bài tập cuối chương 5 hay, chi tiết khác:
Bài 1 trang 120 Toán 8 Tập 1: Cho tứ giác ABCD có . Khi đó, bằng ....
Bài 2 trang 120 Toán 8 Tập 1: Cho hình thang cân ABCD có AB // CD, . Khi đó, bằng ....