Bài 3 trang 104 Toán 8 Tập 1 Cánh diều

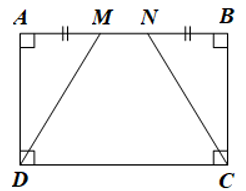
Cho hình chữ nhật ABCD. Trên cạnh AB lấy hai điểm M, N sao cho AM = NB < AB. Chứng minh tứ giác MNCD là hình thang cân.

Giải Toán 8 Bài 3: Hình thang cân - Cánh diều

Bài 3 trang 104 Toán 8 Tập 1: Cho hình chữ nhật ABCD. Trên cạnh AB lấy hai điểm M, N sao cho AM = NB < $\frac{1}{2}$AB. Chứng minh tứ giác MNCD là hình thang cân.

Lời giải:

Do ABCD là hình chữ nhật nên AD = BC, $\widehat{DAM}=\widehat{CBN}=90°$ và AB // CD.

Xét ΔAMD và ΔBNC có:

$\widehat{DAM}=\widehat{CBN}=90°$ (chứng minh trên);

AD = BC (chứng minh trên);

AM = BN (giả thiết).

Do đó ΔAMD = ΔBNC (hai cạnh góc vuông).

Suy ra $\widehat{AMD}=\widehat{BNC}$ (hai góc tương ứng).

Mặt khác $\widehat{AMD}+\widehat{DMN}=180°,\widehat{BNC}+\widehat{CNM}=180°$ (kề bù)

Suy ra $\widehat{DMN}=\widehat{CNM}$.

Tứ giác MNCD có MN // CD (do AB // CD) nên là hình thang.

Lại có $\widehat{DMN}=\widehat{CNM}$ 

Suy ra hình thang MNCD là hình thang cân.

Lời giải bài tập Toán 8 Bài 3: Hình thang cân hay, chi tiết khác:

• Khởi động trang 101 Toán 8 Tập 1: Ở lớp 6, phần Hình học trực quan, chúng ta đã được làm quen với hình thang cân và những vật thể có dạng hình thang cân ....

• Hoạt động 1 trang 101 Toán 8 Tập 1: Cho biết hai cạnh AB và CD của tứ giác ABCD ở Hình 22 có song song với nhau hay không ....

• Hoạt động 2 trang 101 Toán 8 Tập 1: Hai góc C và D cùng kề với đáy CD của hình thang ABCD ở Hình 23. Cho biết hai góc C và D có bằng nhau hay không ....

• Hoạt động 3 trang 102 Toán 8 Tập 1: Cho hình thang cân ABCD có AB // CD, AB < CD, E là giao điểm của AD và BC (Hình 25) ....

• Luyện tập 1 trang 102 Toán 8 Tập 1: Cho hình thang cân ABCD có AB // CD. Chứng minh $\widehat{ADB}=\widehat{BCA}$ ....

• Hoạt động 4 trang 102, 103 Toán 8 Tập 1: Quan sát hình thang ABCD (AB // CD, AB < CD) có hai đường chéo AC và BD bằng nhau. Kẻ BE song song với AC ....

• Luyện tập 2 trang 103 Toán 8 Tập 1: Một ô cửa sổ có dạng hình chữ nhật với chiều dài là 120 cm và chiều rộng là 80 cm. Người ta mở rộng ô cửa sổ đó bằng cách tăng độ dài cạnh dưới về hai bên ....

• Bài 1 trang 103 Toán 8 Tập 1: Cho hình thang cân ABCD có AB // CD, AB < CD. Gọi M, N lần lượt là trung điểm của AB, CD và T là giao điểm của AC và BD ....

• Bài 2 trang 104 Toán 8 Tập 1: Người ta ghép ba hình tam giác đều có độ dài cạnh là a với vị trí như Hình 31 ....

• Bài 4 trang 104 Toán 8 Tập 1: Cho tam giác ABC cân tại A có hai đường phân giác BE và CK. Chứng minh tứ giác BKEC là hình thang cân ....

• Bài 5 trang 104 Toán 8 Tập 1: Hình 33a là mặt cắt đứng phần chứa nước của một con mương (Hình 32) khi đầy nước có dạng hình thang cân ....