Bài 5 trang 104 Toán 8 Tập 1 Cánh diều
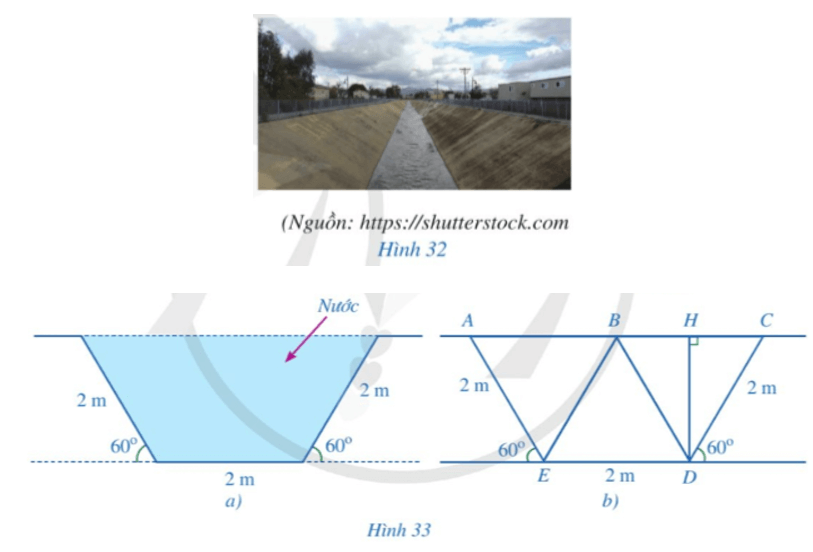
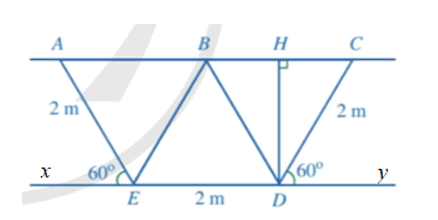
Hình 33a là mặt cắt đứng phần chứa nước của một con mương (Hình 32) khi đầy nước có dạng hình thang cân. Người ta mô tả lại bằng hình học mặt cắt đứng của con mương đó ở Hình 33b với BD // AE (B thuộc AC), H là hình chiếu của D trên đường thẳng AC.
Giải Toán 8 Bài 3: Hình thang cân - Cánh diều
Bài 5 trang 104 Toán 8 Tập 1: Hình 33a là mặt cắt đứng phần chứa nước của một con mương (Hình 32) khi đầy nước có dạng hình thang cân. Người ta mô tả lại bằng hình học mặt cắt đứng của con mương đó ở Hình 33b với BD // AE (B thuộc AC), H là hình chiếu của D trên đường thẳng AC.
a) Chứng minh các tam giác BCD, BDE, ABE là các tam giác đều.
b) Tính độ dài của DH, AC.
c) Tính diện tích mặt cắt đứng phần chứa nước của con mương đó khi đầy nước.
Lời giải:
a) • Do BD // AE nên (đồng vị)
Do AC // ED nên và (các cặp góc so le trong).
Ta có
Suy ra
ΔBCD có nên là tam giác đều.
Suy ra BD = BC = CD = 2 m.
• ΔBDE có BD = DE = 2 m nên là tam giác cân tại D
Lại có nên ΔBDE là tam giác đều.
Suy ra BE = BD = DE = 2 m và .
• Do AC // ED nên (so le trong).
ΔABE có AE = BE = 2 m nên là tam giác cân tại E.
Lại có nên ΔABE là tam giác đều.
b) • Do ΔBCD là tam giác đều nên đường cao BH đồng thời là đường trung tuyến của tam giác
Do đó H là trung điểm của BC nên .
Xét ΔDHC vuông tại H, theo định lí Pythagore có:
CD2 = HC2 + DH2
Suy ra DH2 = CD2 – HC2 = 22 – 12 = 3.
Do đó DH = (m).
• Do ΔABE là tam giác đều nên AB = AE = 2 m.
Khi đó AC = AB + BC = 2 + 2 = 4 (m).
c) Diện tích mặt cắt đứng phần chứa nước của con mương đó khi đầy nước là:
.
Lời giải bài tập Toán 8 Bài 3: Hình thang cân hay, chi tiết khác: