Bài 6 trang 78 Toán 8 Tập 2 Cánh diều

Cho hình bình hành ABCD và BMNP như ở . Chứng minh:

Giải Toán 8 Bài 6: Trường hợp đồng dạng thứ nhất của tam giác - Cánh diều

Bài 6 trang 78 Toán 8 Tập 2: Cho hình bình hành ABCD và BMNP như ở Hình 67. Chứng minh:

a) $\frac{BM}{BA} = \frac{BP}{BC};$

b) ∆MNP ᔕ ∆CBA.

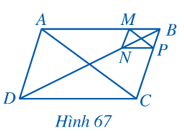
Lời giải:

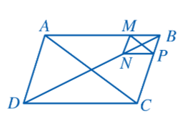
a) Do ABCD là hình bình hành nên AD // BC và AB // CD.

Do BMNP là hình bình hành nên MN // BP và NP // BM

Do đó MN // BC // AD và NP // AB // CD.

Xét ∆ABDvới MN // AD, ta có $\frac{BM}{BA} = \frac{BN}{BD} = \frac{MN}{AD}$ (hệ quả của định lí Thalès) (1)

Xét ∆BDCvới NP // CD, ta có $\frac{BP}{BC} = \frac{BN}{BD} = \frac{NP}{CD}$ (hệ quả của định lí Thalès) (2)

Do đó $\frac{BM}{BA} = \frac{BP}{BC} .$

b) Xét tam giác ABC có: $\frac{BM}{BA} = \frac{BP}{BC}$ nên MP // AC (định lí Thalès đảo)

Suy ra $\frac{BM}{BA} = \frac{BP}{BC} = \frac{MP}{AC}$ (hệ quả của định lí Thalès) (3)

Vì ABCD là hình bình hành nên AD = CB; BA = CD(4)

Tư (1), (2), (3) và (4) ta có $\frac{MN}{CB} = \frac{NP}{BA} = \frac{MP}{CA}$

Lời giải bài tập Toán 8 Bài 6: Trường hợp đồng dạng thứ nhất của tam giác hay, chi tiết khác: