Luyện tập 2 trang 78 Toán 8 Tập 2 Cánh diều
Cho , chứng minh tam giác CDM vuông tại M.
Giải Toán 8 Bài 6: Trường hợp đồng dạng thứ nhất của tam giác - Cánh diều
Luyện tập 2 trang 78 Toán 8 Tập 2: Cho Hình 64, chứng minh tam giác CDM vuông tại M.
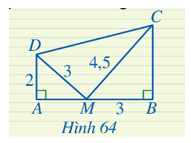
Lời giải:
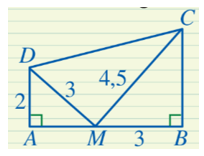
Ta có nên
Xét ∆ADM và ∆BMC có:
Suy ra ∆ADMᔕ∆BMC.
Do đó (hai góc tương ứng)
Mà (tổng hai góc nhọn trong tam giác BCM vuông tại B bằng 90°)
Suy ra
Lại có
Nên
Do đó ∆CDM vuông tại M.
Lời giải bài tập Toán 8 Bài 6: Trường hợp đồng dạng thứ nhất của tam giác hay, chi tiết khác:
Hoạt động 1 trang 74 Toán 8 Tập 2: Quan sát Hình 56 và so sánh các tỉ số ....
Bài 1 trang 78 Toán 8 Tập 2: Quan sát Hình 65 và chỉ ra những cặp tam giác đồng dạng: ....
