Bài 4.16 trang 88 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8

Tam giác ABC có AB = 15 cm, AC = 20 cm, BC = 25 cm. Đường phân giác của góc BAC cắt cạnh BC tại D.

Giải Toán 8 Luyện tập chung - Kết nối tri thức

Bài 4.16 trang 88 Toán 8 Tập 1: Tam giác ABC có AB = 15 cm, AC = 20 cm, BC = 25 cm. Đường phân giác của góc BAC cắt cạnh BC tại D.

a) Tính độ dài các đoạn thẳng DB và DC.

b) Tính tỉ số diện tích của hai tam giác ABD và ACD.

Lời giải:

a)

Áp dụng tính chất đường phân giác, ta có:

$\frac{DB}{DC}=\frac{AB}{AC}=\frac{15}{20}=\frac{3}{4}$.

Suy ra $\frac{DB}{3}=\frac{DC}{4}$ .

Áp dụng tính chất dãy tỉ số bằng nhau, ta có:

$\frac{DB}{3}=\frac{DC}{4}=\frac{DB+DC}{3+4}=\frac{BC}{7}=\frac{25}{7}$.

Do đó, $DB=\frac{25.3}{7}=\frac{75}{7}$ (cm); $DC=\frac{25.4}{7}=\frac{100}{7}$ (cm).

Vậy $DB=\frac{75}{7}$ cm; $DC=\frac{100}{7}$cm.

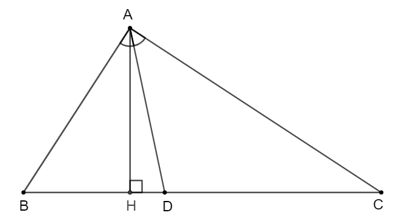
b) Hai tam giác ABD và ACD có chung đường cao kẻ từ đỉnh A đến cạnh BC, ta gọi đường cao đó là AH.

Ta có: $S_{ABD}=\frac{1}{2}AH.DB;S_{ADC}=\frac{1}{2}AH.DC$ .

Suy ra $\frac{S_{ABD}}{S_{ADC}}=\frac{\frac{1}{2}AH.BD}{\frac{1}{2}AH.DC}=\frac{DB}{DC}=\frac{3}{4}$ .

Vậy tỉ số diện tích của hai tam giác ABD và ACD bằng $\frac{3}{4}$.

Lời giải bài tập Toán 8 Luyện tập chung hay, chi tiết khác:

• Bài 4.13 trang 88 Toán 8 Tập 1: Tìm độ dài x trong Hình 4.30 ....

• Bài 4.14 trang 88 Toán 8 Tập 1: Cho tứ giác ABCD, gọi E, F, K lần lượt là trung điểm của AD, BC, AC ....

• Bài 4.15 trang 88 Toán 8 Tập 1: Cho tam giác ABC, phân giác AD (D ∈ BC). Đường thẳng qua D song song với AB cắt AC tại E ....

• Bài 4.17 trang 88 Toán 8 Tập 1: Cho hình bình hành ABCD, một đường thẳng đi qua D cắt AC, AB, CB theo thứ tự tại M, N, K ....