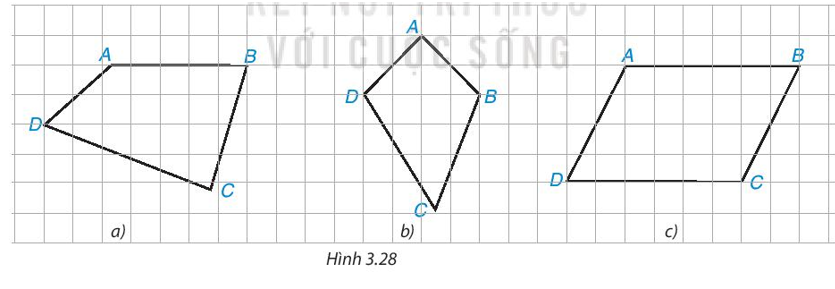
c) Tứ giác có hai cạnh đối nào cũng song song là hình bình hành.
Câu hỏi:
c) Tứ giác có hai cạnh đối nào cũng song song là hình bình hành.
Trả lời:
c) Tứ giác có hai cạnh đối nào cũng song song hay có hai cặp cạnh đối song song nên
tứ giác đó là hình bình hành.
Vậy khẳng định c) đúng.