Cắt một mảnh giấy hình thang cân bằng một nhát thẳng cắt cả hai cạnh đáy thì được

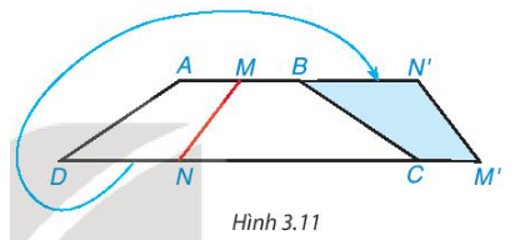
Cắt một mảnh giấy hình thang cân bằng một nhát thẳng cắt cả hai cạnh đáy thì được hai hình thang. Lật một trong hai hình thang đó rồi ghép với hình thang còn lại dọc theo các cạnh bên của hình thang ban đầu (Hình 3.11). Hãy giải thích tại sao hình tạo thành cũng là một hình thang cân.

Sau bài học này ta giải quyết được bài toán như sau:

Ta cắt một mảnh giấy hình thang cân bằng một nhát thẳng cắt cả hai cạnh đáy.

Lật một trong hai hình thang đó rồi ghép với hình thang còn lại dọc theo các cạnh bên của hình thang ban đầu nên $\widehat{D}=\widehat{M}\text{'}$.

Tứ giác ABCD là hình thang cân nên AB // CD suy ra MN’ // M’N.

Do đó MN’M’N là hình thang.

Hình thang MN’M’N có $\widehat{D}=\widehat{M}\text{'}$ nên MN’M’N là hình thang cân.