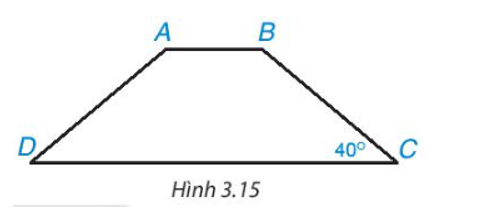
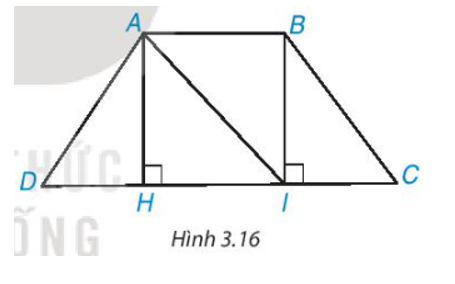
b) Chứng minh tam giác AHD = tam giác BIC, từ đó suy ra AD = BC.
Câu hỏi:
b) Chứng minh ∆AHD = ∆BIC, từ đó suy ra AD = BC.
Trả lời:
b) Vì ABCD là hình thang cân (AC // CD) nên AD = BC; .
Xét ∆AHD và ∆BIC có:
(vì AH ⊥ DC, BI ⊥ DC, H ∈ CD, I ∈ CD);
AD = BC (chứng minh trên);
(chứng minh trên).
Do đó ∆AHD = ∆BIC (cạnh huyền – góc nhọn).
Suy ra AD = BC (hai cạnh tương ứng).