Cho hình bình hành ABCD. Lấy điểm E sao cho B là trung điểm của AE, lấy điểm F sao cho

Câu hỏi:

Cho hình bình hành ABCD. Lấy điểm E sao cho B là trung điểm của AE, lấy điểm F sao cho C là trung điểm của DF. Chứng minh rằng:

a) Hai tứ giác AEFD, ABFC là những hình bình hành;

Trả lời:

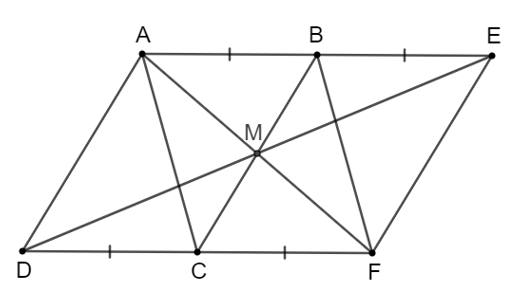
a) Vì ABCD là hình bình hành nên AB = CD; AB // CD.

Mà hai điểm B, C lần lượt là trung điểm AE, DF.

Suy ra AE = DF; AB = BE = CD = CF.

Tứ giác AEFD có AE // DF (vì AB // CD); AE = DF (chứng minh trên).

Do đó tứ giác AEFD là hình bình hành.

Tứ giác ABFC có AB // CF (vì AB // CD); AB = CF (chứng minh trên).

Do đó tứ giác ABFC là hình bình hành.

Vậy ta chứng minh được hai tứ giác AEFD, ABFC là những hình bình hành.

Câu 1:

Trong các tứ giác ở Hình 3.39, tứ giác nào là hình bình hành? Vì sao?

Câu 2:

Cho hình bình hành ABCD. Lấy điểm M thuộc cạnh AB và điểm N thuộc cạnh CD sao cho AM = CN. Chứng minh rằng:

a) AN = CM;

Câu 3:

b) $\hat{A M C} = \hat{A N C}$

Câu 4:

Vẽ tứ giác ABCD theo hướng dẫn sau:

Bước 1. Vẽ đoạn thẳng AB và đường thẳng a song song với AB.

Bước 2. Lấy điểm C ∈ a.

Bước 3. Trên a chọn D sao cho CD = AB và A, D nằm cùng phía đối với BC.

Hãy giải thích tại sao tứ giác ABCD là hình bình hành.

Câu 5:

b) Các trung điểm của ba đoạn thẳng AF, DE, BC trùng nhau.

Câu 6:

Cho ba điểm không thẳng hàng.

a) Tìm một điểm sao cho nó cùng với ba điểm đã cho là bốn đỉnh của một hình bình hành.

Câu 7:

b) Hỏi tìm được bao nhiêu điểm như vậy?