Cho hình bình hành ABCD, một đường thẳng đi qua D cắt AC, AB, CB theo

Cho hình bình hành ABCD, một đường thẳng đi qua D cắt AC, AB, CB theo thứ tự tại M, N, K. Chứng minh rằng: DM² = MN . MK.

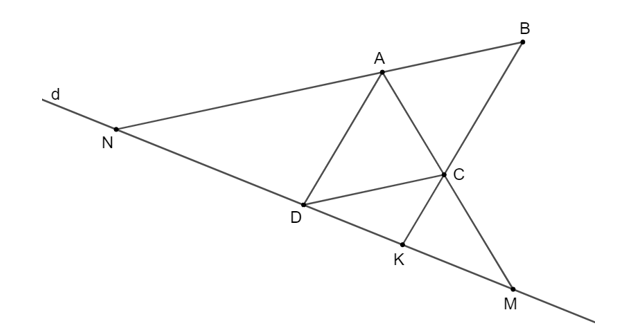
Vì ABCD là hình bình hành nên AB // CD, AD // BC suy ra AN // cD, ad // ck.

Áp dụng định lí Thalès vào tam giác AMN có AN // CD, ta được:

$\frac{DM}{MN}=\frac{CM}{AM}$           (1)

Áp dụng định lí Thalès vào tam giác ADM có CK // AD, ta được:

$\frac{MK}{DM}=\frac{CM}{AM}$           (2)

Từ (1) và (2) suy ra: $\frac{DM}{MN}=\frac{MK}{DM}=\frac{CM}{AM}$.

Do đó DM² = MN . MK (đpcm).