Cho hình thang ABCD (AB // CD) có góc DAB=góc DBC. a) Chứng minh rằng ΔABD ∽ ΔBDC.
Câu hỏi:
Cho hình thang ABCD (AB // CD) có .
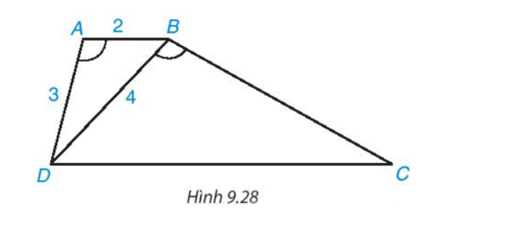
a) Chứng minh rằng ΔABD ∽ ΔBDC.
Trả lời:
a) Vì AB // CD (giả thiết) nên (2 góc ở vị trí so le trong).
+ Xét ΔABD và ΔBDC có: .
Suy ra ΔABD ∽ ΔBDC (g.g).