Cho M là một điểm nằm trong tam giác đều ABC. Qua M kẻ các đường thẳng song song

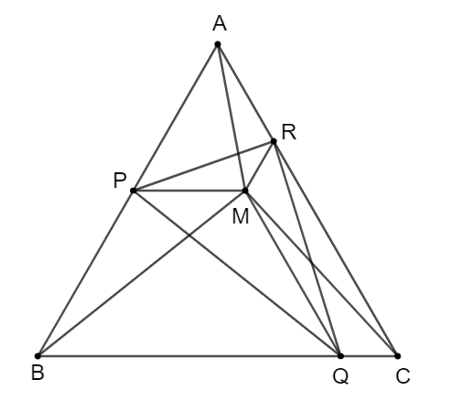
Cho M là một điểm nằm trong tam giác đều ABC. Qua M kẻ các đường thẳng song song với BC, CA, AB lần lượt cắt AB, BC, CA tại các điểm P, Q, R.

a) Chứng minh tứ giác APMR là hình thang cân.

a) Vì tam giác ABC đều nên $\widehat{BAC}=\widehat{ABC}=\widehat{ACB}=60°$.

Vì PM // BC nên $\widehat{ABC}=\widehat{APM}=60°$.

Tứ giác APMR là hình thang (vì MR // AP) có $\widehat{ABC}=\widehat{APM}$.

Do đó tứ giác APMR là hình thang cân.