Cho tam giác ABC vuông tại A và có đường cao AH. Biết rằng BH = 16 cm, CH = 9 cm.

Cho tam giác ABC vuông tại A và có đường cao AH. Biết rằng BH = 16 cm, CH = 9 cm.

a) Tính độ dài đoạn thẳng AH.

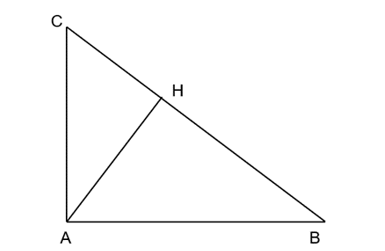
 a) Có BC = BH + CH = 16 + 9 = 25 (cm).

Xét tam giác ABC vuông tại A có: AB² + AC² = BC² (định lý Pythagore).

Xét tam giác AHC vuông tại H có: AC² = AH² + CH² (định lý Pythagore).

Suy ra AH² = AC² – CH²   (1).

Xét tam giác AHB vuông tại H có: AH² + BH² = AB² (định lý Pythagore).

Suy ra AH² = AB² – BH² (2).

Xét (1) + (2), có:

2AH² = AC² – CH² + AB² – BH² 

2AH² = BC² – CH² – BH²         (vì AB² + AC² = BC²)

2AH² = 25² – 9² – 16²

2AH² = 288

AH² = 144

Suy ra AH = 12 (cm).