Câu hỏi:
Trong Hình 9.72, cho AH, HE, HF lần lượt là các đường cao của các tam giác ABC, AHB, AHC. Chứng minh rằng:
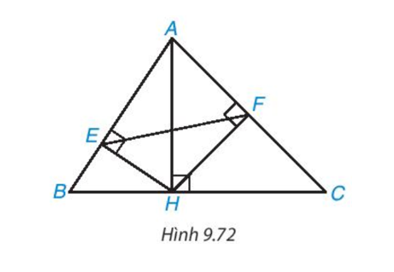
a) ΔAEH ∽ ΔAHB;
Trả lời:
a) Xét hai tam giác AEH (vuông tại E) và tam giác AHB (vuông tại H) có góc BAH chung.
Suy ra ΔAEH ∽ ΔAHB.
Câu 1:
Cho tam giác ABC vuông tại A và có đường cao AH. Biết rằng BH = 16 cm, CH = 9 cm.
a) Tính độ dài đoạn thẳng AH.
Câu 3:
Cho tam giác ABC có AB = 6 cm, AC = 8 cm, BC = 10 cm. Cho điểm M nằm trên cạnh BC sao cho BM = 4 cm. Vẽ đường thẳng MN vuông góc với AC tại N và đường thẳng MP vuông góc với AB tại P.
a) Chứng minh rằng ΔBMP ∽ ΔMCN.
Câu 7:
Cho tam giác ABC vuông tại A có đường cao AH. Cho M và N lần lượt là trung điểm của AB và AC. Chứng minh ΔHBM∽ ΔHAN.
Câu 8:
Vào gần buổi trưa, khi bóng bạn An dài 60 cm thì bóng cột cờ dài 3 m.
a) Biết rằng bạn An cao 1,4 m. Hỏi cột cờ cao bao nhiêu mét?
