Luyện tập 1 trang 65 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8
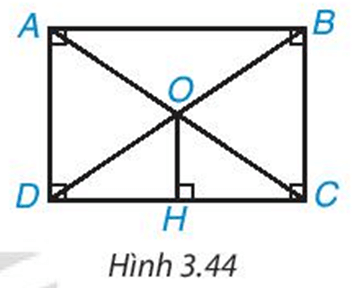
Cho hình chữ nhật ABCD. Hai đường chéo AC, BD cắt nhau tại O. Kẻ OH (H.3.44). Chứng minh rằng H là trung điểm của DC.
Giải Toán 8 Bài 13: Hình chữ nhật - Kết nối tri thức
Luyện tập 1 trang 65 Toán 8 Tập 1: Cho hình chữ nhật ABCD. Hai đường chéo AC, BD cắt nhau tại O. Kẻ OH ⊥ DC (H ∈ DC)(H.3.44). Chứng minh rằng H là trung điểm của DC.
Lời giải:
Vì ABCD là hình chữ nhật có hai đường chéo AC và BD bằng nhau và cắt nhau tại trung điểm của mỗi đường.
Suy ra OA = OB = OC = OD.
Xét tam giác OCD cân tại O (vì OC = OD) có OH là đường cao nên OH cũng là đường trung tuyến.
Do đó CH = DH.
Vậy H là trung điểm của DC.
Lời giải bài tập Toán 8 Bài 13: Hình chữ nhật hay, chi tiết khác:
HĐ1 trang 64 Toán 8 Tập 1: Trong các hình dưới đây, hình nào là hình chữ nhật? Tại sao? ....
HĐ3 trang 65 Toán 8 Tập 1: Cho hình bình hành ABCD có góc A vuông. Tính các góc B, C, D ....