Giải Toán 8 trang 39 Tập 1 Kết nối tri thức

---

Với Giải Toán 8 trang 39 Tập 1 trong Bài 8: Tổng và hiệu hai lập phương Toán lớp 8 Tập 1 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 8 trang 39.

Giải Toán 8 trang 39 Tập 1 Kết nối tri thức

Luyện tập 2 trang 39 Toán 8 Tập 1:

1. Viết đa thức x³ – 8 dưới dạng tích.

2. Rút gọn biểu thức (3x – 2y)(9x² + 6xy + 4y²) + 8y³.

Lời giải:

1. Ta có x³ – 8 = x³ – 2³ = (x – 2)(x² + 2x + 2²) = (x – 2)(x² + 2x + 4).

Vậy x³ – 8 = (x – 2)(x² + 2x + 4).

2. Ta có (3x – 2y)(9x² + 6xy + 4y²) + 8y³

= (3x – 2y)[(3x)² + 3x . 2y + (2y)²] + 8y³

= (3x)³ – (2y)³ + 8y³

= 27x³ – 8y³ + 8y³ = 27x³.

Vậy (3x – 2y)(9x² + 6xy + 4y²) + 8y³ = 27x³.

Vận dụng trang 39 Toán 8 Tập 1: Giải quyết tình huống mở đầu.

Lời giải:

Tròn đã áp dụng công thức tổng của hai lập phương để đưa về dạng tích như sau:

$x^6+y^6={\left(x^2\right)}^3+{\left(y^2\right)}^3$

= (x²+y²)[(x²)² - x².y² + (y²)² ]

= (x² + y²)(x⁴-x²y²+y⁴).

Bài 2.12 trang 39 Toán 8 Tập 1: Viết các biểu thức sau dưới dạng tổng hay hiệu hai lập phương:

a) (x + 4)(x² – 4x + 16);

b) (4x² + 2xy + y²)(2x – y).

Lời giải:

a) (x + 4)(x² – 4x + 16)

= (x + 4)(x² – x . 4 + 4²)

= x³ + 4³ = x³ + 64;

b) (4x² + 2xy + y²)(2x – y) = (2x – y)[(2x)² + 2xy + y²]

= (2x)³ – y³ = 8x³ – y³.

Bài 2.13 trang 39 Toán 8 Tập 1: Thay bằng biểu thức thích hợp.

a) x³ + 512 = (x+8)(x² - + 64);

b) 27x³ - 8y³ = ( - 2y)( + 6xy + 4y²).

Lời giải:

a) Ta có x³ + 512 = x³ + 8³ = (x + 8)(x² – 8x + 8²)

= (x + 8)(x² – 8x + 64).

Vậy ta điền như sau x³ + 512 = (x + 8)(x² – + 64) ;

b) Ta có 27x³ – 8y³ = (3x)³ – (2y)³ = (3x – 2y)[(3x)² + 3x . 2y + (2y)²]

= (3x – 2y)(9x² + 6xy + 4y²).

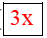
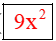
Vậy ta điền như sau 27x³ – 8y³ = ( – 2y)[ + 6xy + 4y²].

Bài 2.14 trang 39 Toán 8 Tập 1: Viết các đa thức sau dưới dạng tích:

a) 27x³ + y³;

b) x³ – 8y³.

Lời giải:

a) 27x³ + y³ = (3x)³ + y³ = (3x + y)[(3x)² – 3x . y + y²]

= (3x + y)(9x² – 3xy + y²).

b) x³ – 8y³ = x³ – (2y)³

= (x – 2y)[x² + x . 2y + (2y)²]

= (x – 2y)(x² + 2xy + 4y²).

Bài 2.15 trang 39 Toán 8 Tập 1: Rút gọn biểu thức sau:

(x – 2y)(x² + 2xy + 4y²) + (x + 2y)(x² – 2xy + 4y²).

Lời giải:

(x – 2y)(x² + 2xy + 4y²) + (x + 2y)(x² – 2xy + 4y²)

= x³ – (2y)³ + x³ + (2y)³

= (x³ + x³) + [(2y)³ – (2y)³]

= x³ + x³ = 2x³.

Lời giải bài tập Toán 8 Bài 8: Tổng và hiệu hai lập phương Kết nối tri thức hay khác:

• Giải Toán 8 trang 37

• Giải Toán 8 trang 38