Giải Toán 8 trang 44 Tập 1 Kết nối tri thức

---

Với Giải Toán 8 trang 44 Tập 1 trong Bài 9: Phân tích đa thức thành nhân tử Toán lớp 8 Tập 1 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 8 trang 44.

Giải Toán 8 trang 44 Tập 1 Kết nối tri thức

Luyện tập 3 trang 44 Toán 8 Tập 1: Phân tích đa thức 2x² – 4xy + 2y – x thành nhân tử.

Lời giải:

Ta phân tích đa thức 2x² – 4xy + 2y – x thành nhân tử như sau:

Cách 1:

2x² – 4xy + 2y – x

= (2x² – 4xy) + (2y – x)

= 2x(x – 2y) – (x – 2y)

= (x – 2y)(2x – 1).

Cách 2:

2x² – 4xy + 2y – x

= (2x² – x) – (4xy – 2y)

= x(2x – 1) – 2y(2x – 1)

= (2x – 1)(x – 2y).

Vận dụng 2 trang 44 Toán 8 Tập 1: Tính nhanh giá trị của biểu thức

A = x² + 2y – 2x – xy tại x = 2022, y = 2020.

Lời giải:

Ta có thể phân tích đa thức A thành nhân tử theo 2 cách như sau:

Cách 1:

Ta có A = x² + 2y – 2x – xy = (x² – 2x) + (2y – xy)

= x(x – 2) + y(2 – x) = x(x – 2) – y(x – 2)

= (x – 2)(x – y).

Cách 2:

Ta có A = x² + 2y – 2x – xy = (x² – xy) – (2x – 2y)

= x(x – y) – 2(x – y) = (x – y)(x – 2).

Thay x = 2022, y = 2020 vào biểu thức A, ta được:

(2022 – 2)(2022 – 2020) = 2020 . 2 = 4040.

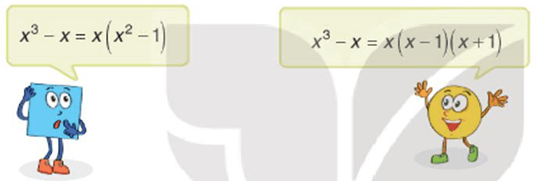
Tranh luận trang 44 Toán 8 Tập 1: Phân tích đa thức x³ – x thành nhân tử.

Em hãy nêu ý kiến của em về lời giải của Tròn và Vuông.

Lời giải:

Bạn Vuông phân tích đa thức đã cho thành tích của hai đa thức, tuy nhiên đa thức trong ngoặc còn có thể phân tích tiếp được.

Bạn Tròn phân tích đa thức thành các nhân tử, trong đó mỗi nhân tử không phân tích tiếp được nữa.

Bài 2.22 trang 44 Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:

a) x² + xy;

b) 6a²b – 18ab;

c) x³ – 4x;

d) x⁴ – 8x.

Lời giải:

a) x² + xy = x(x + y);

b) 6a²b – 18ab = 6ab(a – 3);

c) x³ – 4x = x(x² – 4) = x(x + 2)(x – 2);

d) x⁴ – 8x = x(x³ – 8) = x(x³ – 2³)

= x(x – 2)(x² + 2x + 2²)

= x(x – 2)(x² + 2x + 4).

Bài 2.23 trang 44 Toán 8 Tập 1: Phân tích các đa thức sau thành nhân tử:

a) x² – 9 + xy + 3y;

b) x²y + x² + xy – 1.

Lời giải:

a) x² – 9 + xy + 3y = (x² – 9) + (xy + 3y)

= (x + 3)(x – 3) + y(x + 3)

= (x + 3)(x + y – 3).

b) x²y + x² + xy – 1 = (x²y + xy) + (x² – 1)

= xy(x + 1) + (x + 1)(x – 1) = (x + 1)(xy + x – 1).

Bài 2.24 trang 44 Toán 8 Tập 1: Tìm x, biết:

a) x² – 4x = 0;

b) 2x³ – 2x = 0.

Lời giải:

a) x² – 4x = 0

x(x – 4) = 0

x = 0 hoặc x – 4 = 0

x = 0 hoặc x = 4.

Vậy x ∈ {0; 4}.

b) 2x³ – 2x = 0

2x(x² – 1) = 0

2x(x + 1)(x – 1) = 0

x = 0 hoặc x + 1 = 0 hoặc x – 1 = 0

x = 0 hoặc x = – 1 hoặc x = 1.

Vậy x ∈ {– 1; 0; 1}.

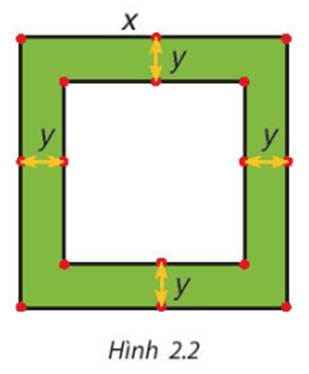
Bài 2.25 trang 44 Toán 8 Tập 1: Một mảnh vườn hình vuông có độ dài cạnh bằng x (mét). Người ta làm đường đi xung quanh mảnh vườn, có độ rộng như nhau và bằng y (mét) (H.2.2).

a) Viết biểu thức tính diện tích S của đường bao quanh mảnh vườn theo x và y.

b) Phân tích S thành nhân tử rồi tính S khi x = 102 m, y = 2 m.

Lời giải:

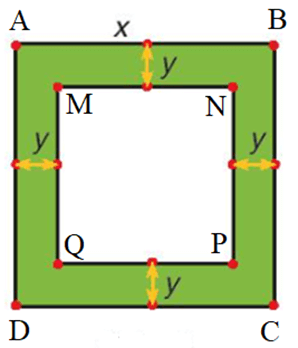
a) Đặt tên các điểm A, B, C, D, M, N, P, Q như hình vẽ.

Diện tích hình vuông ABCD là: x² (m).

Hình vuông MNPQ có độ dài một cạnh là: x – y – y = x – 2y (m).

Diện tích hình vuông MNPQ là: (x – 2y)² (m²).

Diện tích S của đường bao quanh mảnh vườn là:

S = x² – (x – 2y)² = x² – (x² – 4xy + 4y²)

= x² – x² + 4xy – 4y² = 4xy – 4y² (m²).

Vậy diện tích S của đường bao quanh mảnh vườn là 4xy – 4y² (m²).

b) Phân tích đa thức S thành nhân tử, ta được:

S = 4xy – 4y² = 4y(x – y).

Thay x = 102 m, y = 2 m vào biểu thức S, ta được:

S = 4 . 2 . (102 – 2) = 8 . 100 = 800 (m²).

Lời giải bài tập Toán 8 Bài 9: Phân tích đa thức thành nhân tử Kết nối tri thức hay khác:

• Giải Toán 8 trang 42