b) góc NCP= góc NCB+ góc PCD= 45 độ
Câu hỏi:
b)
Trả lời:
b) Xét đường tròn (C; r) có hai tiếp tuyến PM và PD cắt nhau tại P nên PC là tia phân giác của Suy ra
Tương tự, MN và NB là hai tiếp tuyến của đường tròn (C; r) cắt nhau tại N nên CN là tia phân giác của Suy ra
Lại có:
Suy ra nên
Do đó
Vậy
Xem thêm lời giải bài tập Toán 9 Cánh diều hay, chi tiết:
Câu 1:
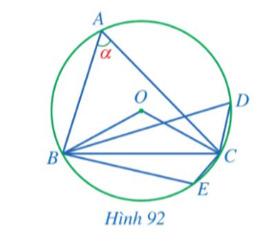
Trong Hình 92, cho các điểm A, B, C, D, E thuộc đường tròn (O).
a) Số đo góc BOC là
Xem lời giải »
Câu 4:
a) Độ dài cung tròn có số đo 30° của đường tròn bán kính R là:
Xem lời giải »
Câu 5:
Chứng minh trong một đường tròn:
a) Đường kính vuông góc với một dây thì đi qua trung điểm của dây ấy;
Xem lời giải »
Câu 6:
b) Đường kính đi qua trung điểm của một dây không đi qua tâm thì vuông góc với dây ấy;
Xem lời giải »