Bài 1 trang 109 Toán 9 Tập 1 Cánh diều
Ròng rọc là một loại máy cơ đơn giản có rãnh và có thể quay quanh một trục, được sử dụng rộng rãi trong công việc nâng lên và hạ xuống vật nặng trong cuộc sống. Trong , có một sợi dây không dãn vắt qua ròng rọc.
Giải Toán 9 Bài 3: Tiếp tuyến của đường tròn - Cánh diều
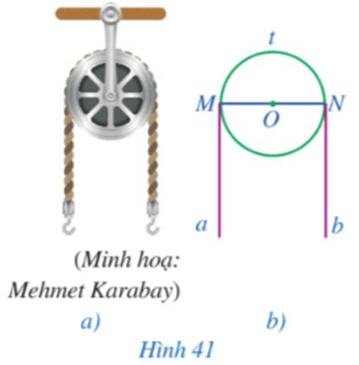
Bài 1 trang 109 Toán 9 Tập 1: Ròng rọc là một loại máy cơ đơn giản có rãnh và có thể quay quanh một trục, được sử dụng rộng rãi trong công việc nâng lên và hạ xuống vật nặng trong cuộc sống. Trong Hình 41a, có một sợi dây không dãn vắt qua ròng rọc.
Giả sử ròng rọc được minh họa bởi đường tròn (O), sợi dây vắt qua ròng rọc được minh họa bởi nửa đường tròn MtN và hai tiếp tuyến Ma, Nb của đường tròn (O) (Hình 41b). Chứng minh Ma // Nb.
Lời giải:
Do Ma, Nb là các tiếp tuyến của đường tròn (O) tại M nên Ma ⊥ OM tại M và Nb ⊥ ON tại N.
Mà MtN là nửa đường tròn nên MN là đường kính đi qua tâm O.
Do đó Ma ⊥ MN và Nb ⊥ MN, suy ra Ma // Nb.
Lời giải bài tập Toán 9 Bài 3: Tiếp tuyến của đường tròn hay, chi tiết khác:
Hoạt động 1 trang 106 Toán 9 Tập 1: Cho đường thẳng a là tiếp tuyến của đường tròn (O; R) ....
Luyện tập 1 trang 107 Toán 9 Tập 1: Cho ba điểm A, B, C thẳng hàng, trong đó B nằm giữa A và C ....
Luyện tập 3 trang 108 Toán 9 Tập 1: Cho hai đường tròn (O), (O’) cắt nhau tại hai điểm A, B ....
Luyện tập 4 trang 109 Toán 9 Tập 1: Cho đường tròn (O; R) và điểm M nằm ngoài đường tròn ....
Bài 2 trang 109 Toán 9 Tập 1: Cho đường tròn (O) và dây AB. Điểm M nằm ngoài đường tròn (O) ....
Bài 3 trang 110 Toán 9 Tập 1: Cho đường tròn (O) và điểm M nằm ngoài đường tròn ....
Bài 5 trang 110 Toán 9 Tập 1: Cho đường tròn (O; R) đường kính AB và các đường thẳng m, n, p ....