Bài 2 trang 117 Toán 9 Tập 1 Cánh diều

Giải Toán 9 Bài 4: Góc ở tâm. Góc nội tiếp - Cánh diều

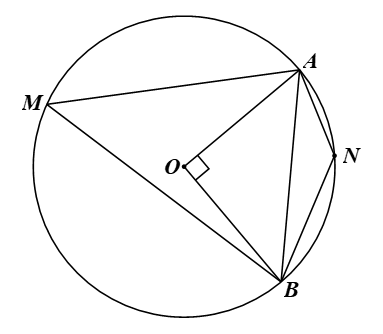
Bài 2 trang 117 Toán 9 Tập 1: Cho đường tròn (O; R) và dây AB sao cho $\widehat{AOB}=90°.$ Giả sử M, N lần lượt là các điểm thuộc cung lớn AB và cung nhỏ AB (M, N khác A và B).

a) Tính độ dài đoạn thẳng AB theo R.

b) Tính số đo các góc ANB và AMB.

Lời giải:

a) Xét đường tròn (O: R) có A, B thuộc đường tròn nên OA = OB = R.

Xét ∆AOB vuông tại O, theo định lí Pythagore, ta có:

AB² = OA² + OB² = R² + R² = 2R².

Do đó: AB = $\sqrt{2R^2}=R\sqrt{2}.$

b) Xét đường tròn (O) có $\widehat{AOB}$ là góc ở tâm chắn cung ANB nên $sđ\stackrel{⏜}{ANB}=\widehat{AOB}=90°.$

Ta có: $sđ\stackrel{⏜}{AMB}=360°-sđ\stackrel{⏜}{ANB}=360°-90°=270°.$

Vì $\widehat{ANB}$ là góc nội tiếp chắn cung AMB nên $\widehat{ANB}=\frac{1}{2}sđ\stackrel{⏜}{AMB}=\frac{1}{2}\cdot 270°=135°.$

Vì $\widehat{AMB}$ là góc nội tiếp chắn cung ANB nên $\widehat{AMB}=\frac{1}{2}sđ\stackrel{⏜}{ANB}=\frac{1}{2}\cdot 90°=45°.$

Lời giải bài tập Toán 9 Bài 4: Góc ở tâm. Góc nội tiếp hay, chi tiết khác:

• Khởi động trang 111 Toán 9 Tập 1: Bác Ngọc dự định làm khung sắt cho khuôn cửa sổ ngôi nhà ....

• Hoạt động 1 trang 111 Toán 9 Tập 1: Cho đường tròn (O). Hãy vẽ góc xOy có đỉnh là tâm O ....

• Luyện tập 1 trang 111 Toán 9 Tập 1: Trong Hình 47, coi mỗi khung đồng hồ là một đường tròn ....

• Hoạt động 2 trang 112 Toán 9 Tập 1: Quan sát góc ở tâm AOB (khác góc bẹt) ở Hình 48, cho biết trong hai phần đường tròn được tô màu xanh và màu đỏ ....

• Luyện tập 2 trang 114 Toán 9 Tập 1: Trong Hình 53, tìm số đo của các góc ở tâm $\widehat{BOC};\widehat{DOA}.$ ....

• Hoạt động 3 trang 115 Toán 9 Tập 1: Trong Hình 55, đỉnh của góc AIB có thuộc đường tròn hay không? ....

• Luyện tập 3 trang 115 Toán 9 Tập 1: Hãy vẽ một đường tròn và hai góc nội tiếp trong đường tròn đó ....

• Hoạt động 4 trang 115 Toán 9 Tập 1: Cho góc AIB nội tiếp đường tròn tâm O đường kính IK ....

• Luyện tập 4 trang 116 Toán 9 Tập 1: Cho đường tròn (O; R) và dây cung AB = R. Điểm C thuộc cung lớn AB ....

• Hoạt động 5 trang 116 Toán 9 Tập 1: Quan sát Hình 60 và nêu mối liên hệ giữa ....

• Luyện tập 5 trang 117 Toán 9 Tập 1: Trong Hình 61, gọi I là giao điểm của AD và BC ....

• Bài 1 trang 117 Toán 9 Tập 1: Quan sát Hình 62, hãy cho biết: ....

• Bài 3 trang 117 Toán 9 Tập 1: Trong Hình 63, cho biết AB = OA ....

• Bài 4 trang 117 Toán 9 Tập 1: Biểu đồ hình quạt tròn ở Hình 64 mô tả các thành phần của một chai nước ép hoa quả ....

• Bài 5 trang 117 Toán 9 Tập 1: Cho hai đường tròn (O), (I) cắt nhau tại hai điểm A, B ....

• Bài 6 trang 117 Toán 9 Tập 1: Hãy sử dụng compa và thước thẳng để vẽ tam giác ABC vuông tại A ....