Bài 5 trang 117 Toán 9 Tập 1 Cánh diều
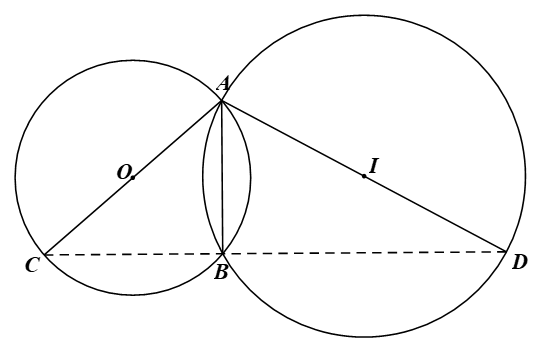
Cho hai đường tròn (O), (I) cắt nhau tại hai điểm A, B. Kẻ các đoạn thẳng AC, AD lần lượt là các đường kính của hai đường tròn (O), (I). Chứng minh ba điểm B, C, D thẳng hàng.
Giải Toán 9 Bài 4: Góc ở tâm. Góc nội tiếp - Cánh diều
Bài 5 trang 117 Toán 9 Tập 1: Cho hai đường tròn (O), (I) cắt nhau tại hai điểm A, B. Kẻ các đoạn thẳng AC, AD lần lượt là các đường kính của hai đường tròn (O), (I). Chứng minh ba điểm B, C, D thẳng hàng.
Lời giải:
Ta có:
⦁ (góc nội tiếp chắn nửa đường tròn (O)).
⦁ (góc nội tiếp chắn nửa đường tròn (I)).
Suy ra hay
Do đó ba điểm B, C, D thẳng hàng.
Lời giải bài tập Toán 9 Bài 4: Góc ở tâm. Góc nội tiếp hay, chi tiết khác:
Khởi động trang 111 Toán 9 Tập 1: Bác Ngọc dự định làm khung sắt cho khuôn cửa sổ ngôi nhà ....
Hoạt động 1 trang 111 Toán 9 Tập 1: Cho đường tròn (O). Hãy vẽ góc xOy có đỉnh là tâm O ....
Luyện tập 1 trang 111 Toán 9 Tập 1: Trong Hình 47, coi mỗi khung đồng hồ là một đường tròn ....
Luyện tập 2 trang 114 Toán 9 Tập 1: Trong Hình 53, tìm số đo của các góc ở tâm ....
Hoạt động 4 trang 115 Toán 9 Tập 1: Cho góc AIB nội tiếp đường tròn tâm O đường kính IK ....
Hoạt động 5 trang 116 Toán 9 Tập 1: Quan sát Hình 60 và nêu mối liên hệ giữa ....
Luyện tập 5 trang 117 Toán 9 Tập 1: Trong Hình 61, gọi I là giao điểm của AD và BC ....
Bài 1 trang 117 Toán 9 Tập 1: Quan sát Hình 62, hãy cho biết: ....