Hoạt động 4 trang 115 Toán 9 Tập 1 Cánh diều

Giải Toán 9 Bài 4: Góc ở tâm. Góc nội tiếp - Cánh diều

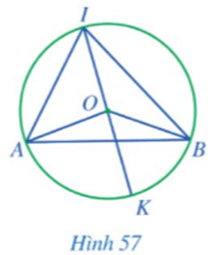
Hoạt động 4 trang 115 Toán 9 Tập 1: Cho góc AIB nội tiếp đường tròn tâm O đường kính IK sao cho tâm O nằm trong góc đó (Hình 57).

a) Các cặp góc $\hat{O A I}$ và $\hat{O I A}$ ; $\hat{O B I}$ và $\hat{O I B}$ có bằng nhau hay không?

b) Tính các tổng $\hat{A O I} + 2 \hat{O I A}, \hat{B O I} + 2 \hat{O I B} .$

c) Tính các tổng $\hat{A O I} + \hat{A O K}, \hat{B O I} + \hat{B O K} .$

d) So sánh $\hat{A O K}$ và $2 \hat{O I A}$ , $\hat{B O K}$ và $2 \hat{O I B}, \hat{A O B}$ và $2 \hat{A I B}$ .

Lời giải:

a) Xét ∆OAI có OA = OI nên ∆OAI cân tại O, suy ra $\hat{O A I} = \hat{O I A} .$

Xét ∆OBI có OB = OI nên ∆OBI cân tại O, suy ra $\hat{O B I} = \hat{O I B} .$

b) Xét ∆OAI có $\hat{A O I} + \hat{O I A} + \hat{O A I} = 180 °$ (định lí tổng các góc của một tam giác).

Do đó $\hat{A O I} + 2 \hat{O I A} = 180 ° .$

Xét ∆OBI có $\hat{B O I} + \hat{O I B} + \hat{O B I} = 180 °$ (định lí tổng các góc của một tam giác).

Do đó $\hat{B O I} + 2 \hat{O I B} = 180 ° .$

c) $\hat{A O I} + \hat{A O K} = 180 °, \hat{B O I} + \hat{B O K} = 180 °$ (các cặp góc kề bù).

d) Ta có $\hat{A O I} + 2 \hat{O I A} = 180 °$ (theo câu b) và $\hat{A O I} + \hat{A O K} = 180 °$ (theo câu c)

Suy ra $\hat{A O K} = 2 \hat{O I A} .$

Ta có $\hat{B O I} + 2 \hat{O I B} = 180 °$ (theo câu b) và $\hat{B O I} + \hat{B O K} = 180 °$ (theo câu c)

Suy ra $\hat{B O K} = 2 \hat{O I B} .$

Ta có: $\hat{A O K} = 2 \hat{O I A}$ và $\hat{B O K} = 2 \hat{O I B}$

Suy ra $\hat{A O K} + \hat{B O K} = 2 \hat{O I A} + 2 \hat{O I B} = 2 (\hat{O I A} + \hat{O I B})$

Do đó $\hat{A O B} = 2 \hat{A I B} .$

Lời giải bài tập Toán 9 Bài 4: Góc ở tâm. Góc nội tiếp hay, chi tiết khác: