Cho hình vuông ABCD cạnh r và đường tròn (C; r). Giả sử M là một điểm nằm trên đường tròn (C; r)
Câu hỏi:
Cho hình vuông ABCD cạnh r và đường tròn (C; r). Giả sử M là một điểm nằm trên đường tròn (C; r) sao cho điểm M nằm trong hình vuông ABCD. Tiếp tuyến của đường tròn (C; r) tại tiếp điểm M cắt các đoạn thẳng AB, AD lần lượt tại N, P. Chứng minh:
a) Các đường thẳng NB, PD là các tiếp tuyến của đường tròn (C; r).
Trả lời:
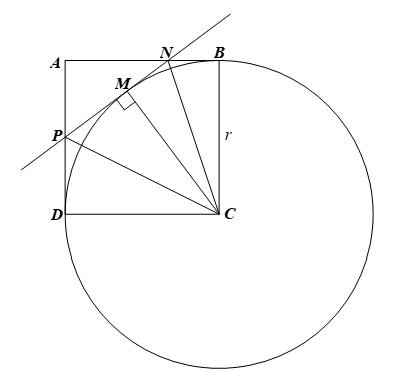
a) Vì ABCD là hình vuông nên ta có
Hay CB ⊥ AB tại B và CD ⊥ AD tại D.
Mà CB và CD là bán kính của đường tròn (C; r) và B ∈ (C; r); D ∈ (C; r).
Suy ra AB, AD là các tiếp tuyến của đường tròn (C; r).
Vậy các đường thẳng NB, PD là các tiếp tuyến của đường tròn (C; r).