Giải Toán 9 trang 60 Tập 1 Cánh diều

---

Với Giải Toán 9 trang 60 Tập 1 trong Bài 2: Một số phép tính về căn bậc hai của số thực Toán lớp 9 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 60.

Giải Toán 9 trang 60 Tập 1 Cánh diều

Bài 6 trang 60 Toán 9 Tập 1: So sánh:

a) $\sqrt{3}\cdot \sqrt{7}$ và $\sqrt{22};$

b) $\frac{\sqrt{52}}{\sqrt{2}}$ và 5;

c) 3$\sqrt{7}$ và $\sqrt{65}$.

Lời giải:

a) Ta có: $\sqrt{3}\cdot \sqrt{7}$ = $\sqrt{21}$.

Vì 21 < 22 nên $\sqrt{21}<\sqrt{22}$ hay $\sqrt{3}\cdot \sqrt{7}<\sqrt{22}.$

Vậy $\sqrt{3}\cdot \sqrt{7}<\sqrt{22}.$

b) Ta có: $\frac{\sqrt{52}}{\sqrt{2}}=\sqrt{\frac{52}{2}}=\sqrt{26}$ và 5 = $\sqrt{25}$

Vì 26 > 25 nên $\sqrt{26}>\sqrt{25}$ hay $\frac{\sqrt{52}}{\sqrt{2}}>5.$

Vậy $\frac{\sqrt{52}}{\sqrt{2}}>5.$

c) Ta có: $3\sqrt{7}=\sqrt{3^2\cdot 7}=\sqrt{9\cdot 7}=\sqrt{63}.$

Vì 63 < 65 nên $\sqrt{63}<\sqrt{65}$ hay $3\sqrt{7}<\sqrt{65}.$

Vậy $3\sqrt{7}<\sqrt{65}.$

Bài 7 trang 60 Toán 9 Tập 1: Cho tam giác đều ABC có độ dài cạnh là a. Tính độ dài đường cao AH của tam giác ABC theo a.

Lời giải:

Xét ∆ABC đều có AH là đường cao nên đồng thời là đường trung tuyến của tam giác, do đó H là trung điểm của BC.

Suy ra HC = $\frac{BC}{2}=\frac{a}{2}.$

Xét ∆AHC vuông tại H, theo định lí Pythagore, ta có:

AC² = AH² + HC²

Suy ra AH² = AC² - HC² = a² - ${\left(\frac{a}{2}\right)}^2=a^2-\frac{a^2}{4}=\frac{3a^2}{4}.$

Do đó AH = $\sqrt{\frac{3a^2}{4}}=\frac{\sqrt{3a^2}}{\sqrt{4}}$ = = $\frac{a\sqrt{3}}{2}$(vì a > 0).

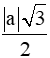
Vậy độ dài đường cao AH của tam giác ABC là $\frac{a\sqrt{3}}{2}$.

Bài 8 trang 60 Toán 9 Tập 1: Trong Vật lí, ta có định luật Joule – Lenz để tính nhiệt lượng toả ra ở dây dẫn khi có dòng điện chạy qua:

Q = I²Rt.

Trong đó: Q là nhiệt lượng toả ra trên dây dẫn tính theo Jun (J);

I là cường độ dòng điện chạy trong dây dẫn tính theo Ampe (A);

R là điện trở dây dẫn tính theo Ohm (Ω);

t là thời gian dòng điện chạy qua dây dẫn tính theo giây.

Áp dụng công thức trên để giải bài toán sau: Một bếp điện khi hoạt động bình thường có điện trở R = 80 Ω. Tính cường độ dòng điện chạy trong dây dẫn, biết nhiệt lượng mà dây dẫn toả ra trong 1 giây là 500 J.

Lời giải:

Theo bài, ta có R = 80 (Ω), t = 1 (s) và Q = 500 (J).

Áp dụng công thức Q = I²RT, ta có: 500 = I².80.1

Suy ra 80I² = 500, nên $I^2=\frac{500}{80}=\frac{25}{4}.$

Do đó I = $\sqrt{\frac{25}{4}}=\frac{\sqrt{25}}{\sqrt{4}}=\frac{5}{2}$ = 2,5 (A) (do I > 0).

Vậy cường độ dòng điện chạy trong dây dẫn là 2,5 Ampe.

Bài 9 trang 60 Toán 9 Tập 1: Tốc độ gần đúng của một ô tô ngay trước khi đạp phanh được tính theo công thức v = $\sqrt{2\lambda gd}$, trong đó v (m/s) là tốc độ của ô tô, d (m) là chiều dài của vết trượt tính từ thời điểm đạp phanh cho đến khi ô tô dừng lại trên đường, λ là hệ số cản lăn của mặt đường, g = 9,8 m/s² (Nguồn: Math for Real Life: Teaching Practical Uses for Algebra, Geometry and Trigonometry, Jim Libby, năm 2017). Nếu một chiếc ô tô để lại vết trượt dài khoảng 20 m trên đường nhựa thì tốc độ của ô tô trước khi đạp phanh là khoảng bao nhiêu mét trên giây (làm tròn kết quả đến hàng đơn vị)? Biết rằng hệ số cản lăn của đường nhựa là λ 0,7.

Lời giải:

Theo bài, ta có λ = 0,7; d = 20 (m) ; g = 9,8 m/s².

Do đó tốc độ của ô tô đó trước khi đạp phanh là:

$v=\sqrt{2\lambda gd}=\sqrt{2\cdot 0,7\cdot 9,8\cdot 20}=\sqrt{274,4}\approx 17\left(m/s\right).$

Vậy tốc độ của ô tô trước khi đạp phanh là khoảng 17 m/s.

Lời giải bài tập Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực hay khác:

• Giải Toán 9 trang 55

• Giải Toán 9 trang 56

• Giải Toán 9 trang 57

• Giải Toán 9 trang 58

• Giải Toán 9 trang 59