Giải Toán 9 trang 86 Tập 1 Cánh diều

---

Với Giải Toán 9 trang 86 Tập 1 trong Bài 2: Một số hệ thức về cạnh và góc trong tam giác vuông Toán lớp 9 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 86.

Giải Toán 9 trang 86 Tập 1 Cánh diều

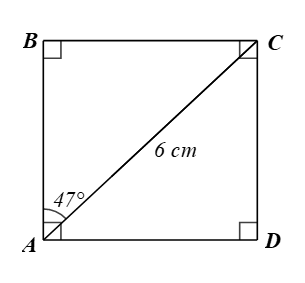
Luyện tập 6 trang 86 Toán 9 Tập 1: Cho hình chữ nhật ABCD thoả mãn AC = 6 cm, $\widehat{BAC}=47°.$ Tính độ dài các đoạn thẳng AB, AD.

Lời giải:

Xét ∆ABC vuông tại B, ta có:

⦁ AB = AC.cos$\widehat{BAC}$ = 6.cos47^o $\approx$4.1 (cm).

⦁ BC = AC.sin$\widehat{BAC}$ = 6.sin47^o $\approx$ 4,4 (cm).

Vì ABCD là hình chữ nhật nên AD = BC ≈ 4,4 cm (tính chất hình chữ nhật).

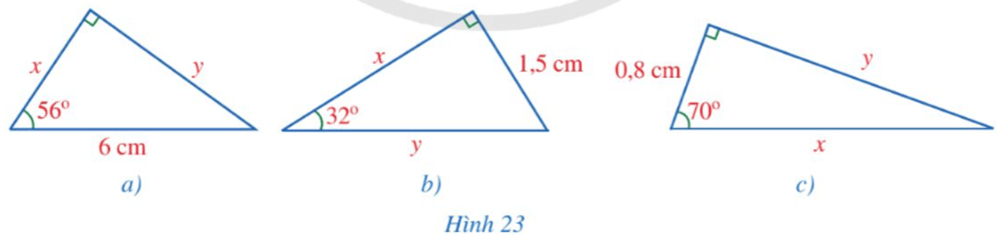
Bài 1 trang 86 Toán 9 Tập 1: Tìm x, y trong mỗi hình 23a, 23b, 23c (làm tròn kết quả đến hàng phần mười của centimét).

Lời giải:

a) Từ hình ta có:

⦁ x = 6.cos56° ≈ 3,4 (cm).

⦁ y = 6.sin56° ≈ 5,0 (cm).

b) Từ hình ta có:

⦁ x = 1,5.cot32° ≈ 2,4 (cm).

⦁ 1,5 = y.sin32°, suy ra $y=\frac{1,5}{\sin 32°}\approx 2,8$ (cm).

c) Từ hình ta có:

⦁ 0,8 = x.cos70°, suy ra $x=\frac{0,8}{\cos 70°}\approx 2,3$ (cm).

⦁ y = 0,8.tan70° ≈ 2,2 (cm).

Bài 2 trang 86 Toán 9 Tập 1: Cho tam giác ABC có đường cao AH = 6 cm, $\hat{B}=40°,\hat{C}=35°.$ Tính độ dài các đoạn thẳng AB, BH, AC, BC (làm tròn kết quả đến hàng phần mười của centimét).

Lời giải:

Xét ∆ABH vuông tại H, ta có:

⦁ sinB = $\frac{AH}{AB}$, suy ra AB = $\frac{AH}{\sin {40}^o}$ = $\frac{6}{\sin 40°}\approx$9,3 (cm).

⦁ BH = AH.cotB = 6.cot40° ≈ 7,2 (cm).

Xét ∆ACH vuông tại H, ta có:

⦁ sinC = $\frac{AH}{AC}$ suy ra AC = $\frac{AH}{\sin 35°}=\frac{6}{\sin 35°}\approx$10,5 (cm).

⦁ CH = AH.cotC = 6.cot35° ≈ 8,6 (cm).

Khi đó, BC = BH + HC ≈ 7,2 + 8,6 = 15,8 (cm).

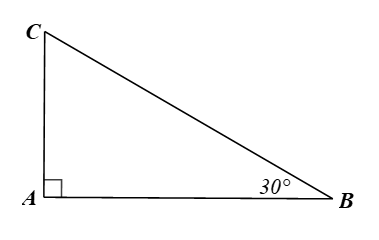
Bài 3 trang 86 Toán 9 Tập 1: Cho tam giác ABC vuông tại A có $\hat{B}=30°.$ Chứng minh AC = $\frac{1}{2}$BC.

Lời giải:

Xét ∆ABC vuông tại A, ta có: AC = BC.sinB = BC.sin30^o = $\frac{1}{2}$BC.

Vậy AC = $\frac{1}{2}$BC.

Lời giải bài tập Toán 9 Bài 2: Một số hệ thức về cạnh và góc trong tam giác vuông hay khác:

• Giải Toán 9 trang 82

• Giải Toán 9 trang 83

• Giải Toán 9 trang 84

• Giải Toán 9 trang 85

• Giải Toán 9 trang 87