Bài 9.26 trang 89 Toán 9 Kết nối tri thức Tập 2 | Giải Toán 9

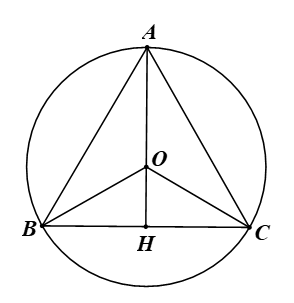
Cho tam giác đều ABC nội tiếp đường tròn (O) bán kính 2 cm. Tính độ dài các cạnh của tam giác ABC.

Giải Toán 9 Bài 30: Đa giác đều - Kết nối tri thức

Bài 9.26 trang 89 Toán 9 Tập 2: Cho tam giác đều ABC nội tiếp đường tròn (O) bán kính 2 cm. Tính độ dài các cạnh của tam giác ABC.

Lời giải:

Vì tam giác đều ABC nội tiếp đường tròn (O) bán kính 2 cm nên ta có OA = OB = OC = 2 cm.

Vì ABC là tam giác đều nên tâm O của đường tròn ngoại tiếp tam giác là trọng tâm của tam giác.

Gọi H là giao điểm của AO và BC. Khi đó AH vừa là đường trung trực, vừa đường cao, vừa là đường trung tuyến của tam giác.

Do đó $A O = \frac{2}{3} A H$ suy ra $A H = \frac{3}{2} A O = \frac{3}{2} \cdot 2 = 3 (cm).$

Vì ∆ABC đều nên $\hat{A B C} = 60 ° .$

Xét ∆ABH vuông tại H, ta có:

$B H = \frac{A H}{\tan \hat{A B H}} = \frac{3}{\tan 60 °} = \frac{3}{\sqrt{3}} = \sqrt{3} (cm).$

Vì AH là đường trung tuyến của ∆ABC nên H là trung điểm của BC, do đó BC = 2BH = 2 $\sqrt{3}$ (cm)

Vậy các cạnh của tam giác ABC có độ dài bằng 2 $\sqrt{3}$ cm.

Lời giải bài tập Toán 9 Bài 30: Đa giác đều hay, chi tiết khác: