Bài 9.29 trang 89 Toán 9 Kết nối tri thức Tập 2 | Giải Toán 9
Liệt kê năm phép quay giữ nguyên một ngũ giác đều nội tiếp một đường tròn tâm O.
Giải Toán 9 Bài 30: Đa giác đều - Kết nối tri thức
Bài 9.29 trang 89 Toán 9 Tập 2: Liệt kê năm phép quay giữ nguyên một ngũ giác đều nội tiếp một đường tròn tâm O.
Lời giải:
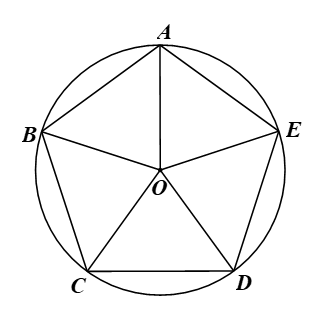
Giả sử ABCDE là ngũ giác đều nội tiếp đường tròn (O) (hình vẽ).
Vì ngũ giác ABCDE nội tiếp đường tròn (O) nên OA = OB = OC = OD = OE.
Vì ABCDE là ngũ giác đều nên AB = BC = CD = DE = EA.
Xét ∆OAB và ∆OBC có:
OA = OB, OB = OC, AB = BC.
Do đó ∆OAB = ∆OBC (c.c.c).
Chứng minh tương tự ta có
∆OAB = ∆OBC = ∆COD = ∆DOE = ∆EOA.
Suy ra
Mà
Do đó
Suy ra
Khi đó phép quay ngược chiều 72° tâm O giữ nguyên điểm O, biến điểm A thành điểm B thuộc đường tròn (O; OA) sao cho tia OA quay ngược chiều kim đồng hồ đến tia OB, điểm A tạo nên cung AB có số đo 72°.
Vậy mỗi phép quay ngược chiều 72° tâm O ở mỗi đỉnh A, B, C, D, E sẽ giữ nguyên ngũ giác đều nội tiếp một đường tròn tâm O.
Lời giải bài tập Toán 9 Bài 30: Đa giác đều hay, chi tiết khác:
HĐ2 trang 87 Toán 9 Tập 2: Để bày bàn ăn cho nhiều người, các nhà hàng thường sử dụng bàn xoay ....
HĐ3 trang 87 Toán 9 Tập 2: Trên bàn xoay tâm O, vẽ tam giác đều ABC nội tiếp một đường tròn (O) ....
Câu hỏi trang 88 Toán 9 Tập 2: a) Phép quay ngược chiều 180° tâm O biến điểm A thành điểm A’ ....
Luyện tập 2 trang 88 Toán 9 Tập 2: Cho hình vuông ABCD nội tiếp đường tròn (O) như Hình 9.50 ....
Thực hành trang 88 Toán 9 Tập 2: Cho điểm O và điểm A khác điểm O (H.9.51) ....
Bài 9.25 trang 89 Toán 9 Tập 2: Trong các hình dưới đây (H.9.53), hình nào vẽ hai điểm M và N ....
Bài 9.26 trang 89 Toán 9 Tập 2: Cho tam giác đều ABC nội tiếp đường tròn (O) bán kính 2 cm ....