Bài 9.27 trang 89 Toán 9 Kết nối tri thức Tập 2 | Giải Toán 9
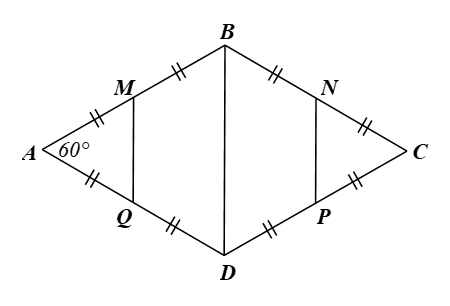
Cho hình thoi ABCD có Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh rằng MBNPDQ là lục giác đều.
Giải Toán 9 Bài 30: Đa giác đều - Kết nối tri thức
Bài 9.27 trang 89 Toán 9 Tập 2: Cho hình thoi ABCD có Gọi M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh rằng MBNPDQ là lục giác đều.
Lời giải:
⦁ Vì ABCD là hình thoi nên AB = BC = CD = DA.
Vì M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA nên MA = MB = AB; NB = NC = BC; PC = PD = CD; QD = QA = DA.
Do đó AM = MB = NB = NC = PC = PD = QD = QA = AB. (1)
Xét ∆ABD có AB = AD nên ∆ABD cân tại A, lại có nên ∆ABD là tam giác đều. Do đó AB = BD (2) và
Lại có M, Q là lần lượt là trung điểm của AB, AD nên MQ là đường trung bình của tam giác. Do đó MQ // BD và MQ = BD. (3)
Chứng minh tương tự, ta cũng có NP = BD. (4)
Từ (1), (2), (3) và (4) suy ra MB = BN = NP = PD = DQ = QM.
⦁ Vì MQ // BD nên (so le trong).
Mà (hai góc kề bù)
Suy ra
Tương tự, ta có
Tam giác BCD có BC = CD và (tính chất hình thoi) nên ∆BCD là tam giác đều. Do đó
Ta có
Khi đó,
Như vậy MBNPDQ có các cạnh bằng nhau và các góc bằng nhau.
Vậy MBNPDQ là lục giác đều.
Lời giải bài tập Toán 9 Bài 30: Đa giác đều hay, chi tiết khác:
HĐ2 trang 87 Toán 9 Tập 2: Để bày bàn ăn cho nhiều người, các nhà hàng thường sử dụng bàn xoay ....
HĐ3 trang 87 Toán 9 Tập 2: Trên bàn xoay tâm O, vẽ tam giác đều ABC nội tiếp một đường tròn (O) ....
Câu hỏi trang 88 Toán 9 Tập 2: a) Phép quay ngược chiều 180° tâm O biến điểm A thành điểm A’ ....
Luyện tập 2 trang 88 Toán 9 Tập 2: Cho hình vuông ABCD nội tiếp đường tròn (O) như Hình 9.50 ....
Thực hành trang 88 Toán 9 Tập 2: Cho điểm O và điểm A khác điểm O (H.9.51) ....
Bài 9.25 trang 89 Toán 9 Tập 2: Trong các hình dưới đây (H.9.53), hình nào vẽ hai điểm M và N ....
Bài 9.26 trang 89 Toán 9 Tập 2: Cho tam giác đều ABC nội tiếp đường tròn (O) bán kính 2 cm ....