Cho đường tròn đường kính BC. Chứng minh rằng với điểm A bất kì (khác B và C) trên
Câu hỏi:
Cho đường tròn đường kính BC. Chứng minh rằng với điểm A bất kì (khác B và C) trên đường tròn, ta đều có: BC < AB + AC < 2BC.
Trả lời:
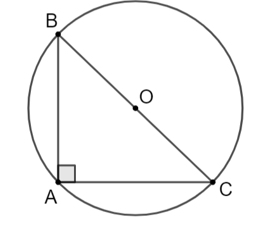
Xét tam giác ABC có: BC < AB + AC (bất đẳng thức tam giác). (1)
Xét đường tròn đường kính BC có dây cung AB, AC ta có: AB < BC, AC < BC.
Suy ra: AB + AC < 2BC. (2)
Từ (1) và (2) suy ra: BC < AB + AC < 2BC.