Toán 9 Bài 16: Vị trí tương đối của đường thẳng và đường tròn - Kết nối tri thức

Người ta gieo một đồng xu hình tròn bán kính 1 cm lên một tờ giấy trải phẳng. Trên tờ giấy đó có vẽ những đường thẳng song song cách đều, tức là những đường thẳng song song mà khoảng cách giữa hai đường thẳng bất kì nằm cạnh nhau luôn bằng nhau. Nếu khoảng cách ấy luôn bằng 2 cm thì có thể xảy ra những trường hợp nào sau đây, vì sao?

a) Đồng xu đè lên một đường thẳng (đồng xu che khuất một phần của đường thẳng).

b) Đồng xu không đè lên đường thẳng nào?

c) Đồng xu đè lên nhiều hơn một đường thẳng.

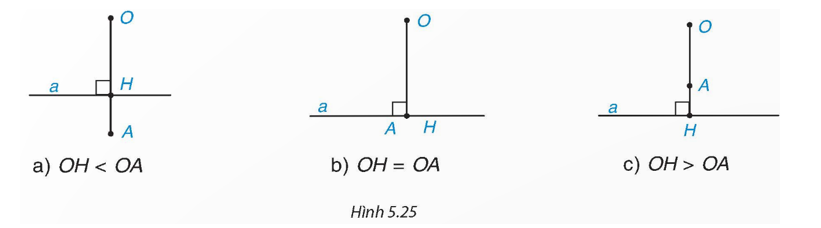
Cho đường thẳng a và điểm O. Gọi H là chân đường vuông góc hạ từ O xuống a, và A là một điểm thuộc tia OH. Trong mỗi trường hợp sau đây, hãy vẽ đường tròn (O; OA) và cho biết đường thẳng a và đường tròn (O; OA) có bao nhiêu điểm chung?

Cho đường thẳng a và điểm O cách a một khoảng bằng 4 cm. Không vẽ hình, hãy dự đoán xem mỗi đường tròn sau cắt, tiếp xúc hay không cắt đường thẳng a. Tại sao?

a) (O; 3 cm).

b) (O; 5 cm).

c) (O; 4 cm).

Cho đoạn thẳng OH và đường thẳng a vuông góc với OH tại H.

a) Xác định khoảng cách từ O đến đường thẳng a.

b) Nếu vẽ đường thẳng (O; OH) thì đường tròn này và đường thẳng a có vị trí tương đối như thế nào?

Cho một hình vuông có độ dài mỗi cạnh bằng 6 cm và hai đường chéo cắt nhau tại I. Chứng minh rằng đường tròn (I; 3 cm) tiếp xúc với cả bốn cạnh của hình vuông.

Cho đường thẳng a và điểm M không thuộc a. Hãy vẽ đường tròn tâm M tiếp xúc với a.

Trở lại tình huống mở đầu. Ở đây, ta hiểu đồng xu nằm đè lên một đường thẳng khi đường tròn (hình ảnh của đồng xu) và đường thẳng ấy cắt nhau.

Bằng cách xét vị trí của tâm đồng xu trong một dải nằm giữa hai đường thẳng song song cạnh nhau (cách đều hoặc không cách đều hai đường thẳng đó), hãy chứng minh rằng chỉ xảy ra các trường hợp a và b, không thể xảy ra trường hợp c.

Cho điểm M ở bên ngoài một đường tròn tâm O. Hãy dùng thước và compa thực hiện các bước vẽ hình như sau:

− Vẽ đường tròn đường kính MO cắt đường tròn (O) tại A và B;

− Vẽ và chứng tỏ các đường thẳng MA và MB là hai tiếp tuyến của (O).

a) MA = MB;

b) MO là tia phân giác của góc AMB;

c) OM là tia phân giác của góc AOB.

Cho góc xMy và điểm A thuộc tia Mx. Hãy vẽ đường tròn tâm O tiếp xúc với cả hai cạnh của góc xMy sao cho A là một trong hai tiếp điểm.

Bạn Thanh cắt 4 hình tròn bằng giấy có bán kính lần lượt là 4 cm, 6 cm, 7 cm và 8 cm để dán trang trí trên một mảnh giấy, trên đó có vẽ trước hai đường thẳng a và b. Biết rằng a và b là hai đường thẳng song song với nhau và cách nhau một khoảng 6 cm (nghĩa là mọi điểm trên đường thẳng b đều cách a một khoảng 6 cm). Hỏi nếu bạn Thanh dán sao cho tâm của cả 4 hình tròn đều nằm trên đường thẳng b thì hình nào đè lên đường thẳng a, hình nào không đè lên đường thẳng a?

Cho đường tròn (O) đi qua ba đỉnh A, B và C của một tam giác cân tại A, Chứng minh rằng đường thẳng đi qua A và song song với BC là một tiếp tuyến của (O).

Cho góc xOy với đường phân giác Ot và điểm A trên cạnh Ox, điểm B trên cạnh Oy sao cho OA = OB. Đường thẳng qua A và vuông góc với Ox cắt Ot tại M. Chứng minh rằng OA và OB là hai tiếp tuyến cắt nhau của đường tròn (M; MA).