Cho tam giác ABC vuông tại A có AB = 3 cm, AC = 4 cm. Chứng minh rằng các điểm A, B, C thuộc
Câu hỏi:
Cho tam giác ABC vuông tại A có AB = 3 cm, AC = 4 cm. Chứng minh rằng các điểm A, B, C thuộc cùng một đường tròn. Tính bán kính của đường tròn đó.
Trả lời:
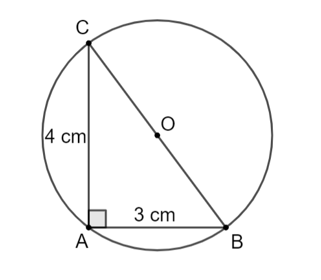
Gọi O là trung điểm của BC.
Ta có AO là trung tuyến ứng với cạnh huyền nên
Suy ra A, B, C cùng thuộc đường tròn bán kính OA.
Tâm O là trung điểm của BC nên BC là đường kính.
Do đó, các điểm A, B, C thuộc cùng một đường tròn.
Xét tam giác ABC vuông tại A, áp dụng định lí Pythagore, ta có:
BC2 = AB2 + AC2 = 32 + 42 = 25.
Suy ra BC = 5 cm.
Khi đó
Vậy các điểm A, B, C thuộc cùng một đường tròn và có bán kính là 2,5 cm.
