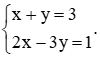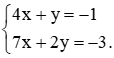Một mảnh vườn được đánh thành nhiều luống, mỗi luống trồng cùng một số cây cải bắp. Hãy tính
Câu hỏi:
Một mảnh vườn được đánh thành nhiều luống, mỗi luống trồng cùng một số cây cải bắp. Hãy tính số cây cải bắp được trồng trên mảnh vườn đó, biết rằng:
– Nếu tăng thêm 8 luống, nhưng mỗi luống trồng ít đi 3 cây cải bắp thì số cải bắp của cả vườn sẽ ít đi 108 cây;
– Nếu giảm đi 4 luống, nhưng mỗi luống trồng thêm 2 cây thì số cải bắp cả vườn sẽ tăng thêm 64 cây.
Trả lời:
Sau bài học này ta giải quyết được bài toán như sau:
Gọi x là số luống trong vườn, y là số cây cải bắp trồng ở mỗi luống (x, y ∈ ℕ*).
– Nếu tăng thêm 8 luống, nhưng mỗi luống trồng ít đi 3 cây cải bắp thì số cải bắp của cả vườn sẽ ít đi 108 cây;
Số luống trong vườn sau khi tăng thêm 8 luống là x + 8 (luống).
Khi mỗi luống trồng ít đi 3 cây cải bắp thì số cây bắp cải ở mỗi luống là: y – 3 (cây).
Số cây cải bắp của cả vườn là: xy (cây).
Theo đề bài, ta có phương trình là:
(x + 8)(y – 3) = xy – 108
xy – 3x + 8y – 24 = xy – 108
3x – 8y = 84. (1)
– Nếu giảm đi 4 luống, nhưng mỗi luống trồng thêm 2 cây thì số cải bắp cả vườn sẽ tăng thêm 64 cây.
Số luống trong vườn sau khi giảm đi 4 luống là x – 4 (luống).
Khi mỗi luống trồng thêm 2 cây cải bắp thì số cây bắp cải ở mỗi luống là: y + 2 (cây).
Số cây cải bắp của cả vườn là: xy (cây).
Theo đề bài, ta có phương trình là:
(x – 4)( y + 2) = xy + 64
xy + 2x – 4y – 8 = xy + 64
2x – 4y = 72
x – 2y = 36. (2)
Từ (1) và (2) ta có hệ phương trình 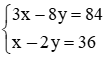 .
.
Từ phương trình thứ hai, ta có x = 2y + 36. Thế vào phương trình thứ nhất, ta được
3(2y + 36) – 8y = 84, tức là 6y + 216 – 8y = 84, suy ra 2y = 132 hay y = 66.
Từ đó x = 2y + 36 = 2 . 66 + 36 = 168.
Số cây cải bắp được trồng trên mảnh vườn đó là: 168 . 66 = 11 088 (cây).
Vậy số cây cải bắp được trồng trên mảnh vườn đó là 11 088 cây.