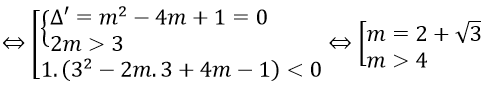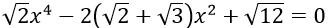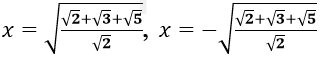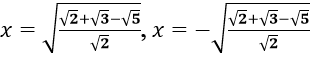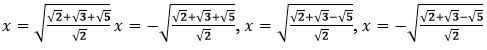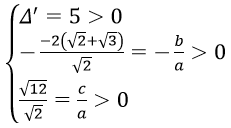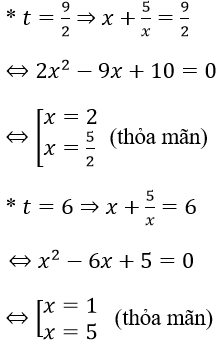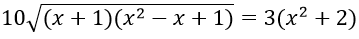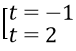Bài tập phương trình quy về phương trình bậc hai chọn lọc, có lời giải - Toán lớp 10

---

Bài tập phương trình quy về phương trình bậc hai chọn lọc, có lời giải

Với Bài tập phương trình quy về phương trình bậc hai chọn lọc, có lời giải Toán lớp 10 tổng hợp 15 bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập phương trình quy về phương trình bậc hai từ đó đạt điểm cao trong bài thi môn Toán lớp 10.

Câu 1. Khẳng định nào đúng về phương trình:

A. vô nghiệm

B. Có 2 nghiệm

C. Có 2 nghiệm

D. Có 4 nghiệm

Câu 2. Phương trình -x⁴ - 2(√2 - 1)x² + (3 - 2√2) = 0 có bao nhiêu nghiệm?

A. 2        B. 3        C. 4        D. 0

Câu 3.Số nghiệm của phương trình 2x⁴ + 3x³ - 16x² + 3x + 2 = 0 là:

A. 1 nghiệm        B. 2 nghiệm        C. 3 nghiệm        D. 4 nghiệm

Câu 4. Số nghiệm của phương trình 2x⁴ - 21x³ + 74x² - 105x + 50 = 0 là:

A. 1 nghiệm        B. 2 nghiệm        C. 3 nghiệm        D. 4 nghiệm

Câu 5. Số nghiệm của phương trình (x+3)⁴ + (x-5)⁴ = 1312 là:

A. 1 nghiệm        B. 2 nghiệm        C. 3 nghiệm        D. 4 nghiệm

Câu 6. Số nghiệm của phương trình (2x-1)(4x+5)(8x+3)(16x-15) = 99x² là:

A. 1 nghiệm        B. 2 nghiệm        C. 3 nghiệm        D. 4 nghiệm

Câu 7. Số nghiệm của phương trình 10√(x³ + 1) = 3(x² + 2) là:

A. 1 nghiệm        B. 2 nghiệm        C. 3 nghiệm        D. 4 nghiệm

Câu 8. Số nghiệm của phương trình 4x(x-1) = |2x-1| + 1 là:

A. 1 nghiệm        B. 2 nghiệm        C. 3 nghiệm        D. 4 nghiệm

Câu 9. Số nghiệm của phương trình 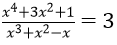là:

A. 1 nghiệm        B. 2 nghiệm        C. 3 nghiệm        D. 4 nghiệm

Câu 10. Cho phương trình ax⁴ + bx² + c = 0 (1) (a ≠ 0). Đặt: Δ = b²-4ac, S = (-b)/a, P = c/a. Ta có (1) vô nghiệm khi và chỉ khi:

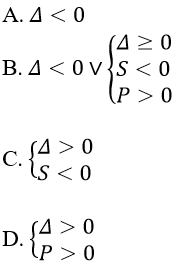
Câu 11. Cho phương trình x⁴ + x² + m = 0. Khẳng định nào sau đây là đúng ?

A. Phương trình có nghiệm ⇔ m ≤ 1/4

B. Phương trình có nghiệmm ≤ 0

C. Phương trình vô nghiệm với mọi m

D. Phương trình có nghiệm duy nhất ⇔ m = -2

Câu 12. Có bao nhiêu giá trị nguyên của a để phương trình: 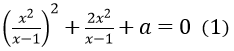có đúng 4 nghiệm.

A. 0        B. 1        C. 2        D. 3

Câu 13. Xác định m để phương trình :(x² + 1/x²) - 2m(x + 1/x) + 1 + 2m = 0 có nghiệm

A. -3/4 ≤ m ≤ 3/4

B. m ≥ 3/4

C. m ≤ -3/4

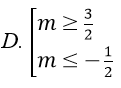
Câu 14. Xác định k để phương trình: x² + 4/x² - 4(x - 2/x) + k - 1 = 0 có đúng hai nghiệm lớn hơn 1:

A. k < -8        B. -8 < k < 1        C. 0 < k < 1        D. Không tồn tại k

Câu 15. Tìm m để phương trình: (x² + 2x + 4)² – 2m(x² + 2x + 4) + 4m – 1 = 0 có đúng hai nghiệm

A. 3 < m < 4

B. m < 2 - √3 ∨ m > 2 + √3

C. 2 + √3 < m < 4

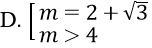
Đáp án và hướng dẫn giải

Câu	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
Đáp án	D	A	D	D	B	D	B	B	D	B	B	A	D	B	D

Câu 1. Chọn D

Đặt t = x² (t ≥ 0)

Phương trình (1) thành √2.t² - 2(√2 + √3)t + √12 = 0  (2)

Ta có Δ' = 5 + 2√6 - 2√6 = 5

Ta có

Suy ra phương trình (2) có 2 nghiệm dương phân biệt

Vậy phương trình (1) có 4 nghiệm

Câu 2. Chọn A

Đặt t = x² (t ≥ 0)

Phương trình (1) thành -t² - 2(√2 - 1)t + (3 - 2√2) = 0 (2)

Phương trình (2) có a.c = (-1)(3 - 2√2) < 0

Suy ra phương trình (2) có 2 nghiệm trái dấu

Suy ra phương trình (2) có 2 nghiệm phân biệt

Câu 3. Chọn D

Ta thấy x = 0 không là nghiệm của phương trình

Với x ≠ 0 ta có PT ⇔ 2x² + 3x - 16 + 3/x + 2/x² = 0 ⇔ 2(x² + 1/x²) + 3(x + 1/x) - 16 = 0

Đặt y = x + 1/x thì y² - 2 = x² + 1/x²

Phương trình trở thành: 2(y² - 2) + 3y - 16 = 0 ⇔ 2y² + 3y - 20 = 0

Phương trình này có nghiệm là y₁ = -4, y₂ = 5/2

Vì vậy x + 1/x = -4 và x+1/x = 5/2 tức là x² + 4x + 1 = 0 và 2x² - 5x + 2 = 0

Từ đó ta tìm đuợc các nghiệm là: x = -2 ± √3, x = 1/2, x = 2

Câu 4. Chọn D

Ta thấy x = 0 không phải là nghiệm của phương trình nên chia hai vế phương trình cho x² ta được:

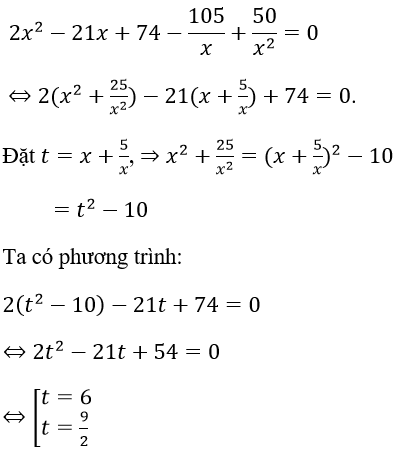
Vậy phương trình có nghiệm là x ∈ {1; 2; 5/2; 5}

Câu 5. Chọn B

Đặt x = t + 1, ta có: (t+4)⁴ + (t-4)⁴ = 1312

⇔ t⁴ + 96t² - 400 = 0 ⇔ t² = 4 ⇔ t = ±2

Suy ra x = 3, x = -1 là nghiệm của phương trình đã cho

Câu 6. Chọn D

Ta thấy x = 0 không là nghiệm của phương trình nên

Phương trình ⇔(32x² + 52x + 15)(32x² - 46x + 15) - 99x² = 0

⇔(36x + 52 + 15/x)(32x - 46 + 15/x) - 99 = 0

Đặt t = 32x + 15/x. Ta có: (t + 52)(t - 46) - 99 = 0 ⇔ t² + 6t - 2491 = 0

⇔ t = 47, t = -53

+ t = 47 ⇔ 32x² - 47x + 15 = 0⇔ x = 1, x = 15/32

+ t = -53 ⇔ 32x² - 53x + 15 = 0⇔ x = (53 ± √889)/64

Vậy tập nghiệm phương trình đã cho là: {1, 15/32, (53±√889)/64}

Câu 7. Chọn B

ĐKXĐ: x³ + 1 ≥ 0 ⇔ x ≥ -1

Phương trình ⇔

Đặt √(x+1) = a, √(x² - x + 1) = b, a ≥ 0, b ≥ 0

Suy ra a² + b² = x² + 2 khi đó

Phương trình trở thành

10ab = 3(a² + b²) ⇔ 3a² - 10ab + 3b² = 0 ⇔ (3a-b)(a-3b) = 0

⇔

Với 3a = b ta có 3√(x+1) = √(x² - x + 1) ⇔ 9(x+1) = x² - x + 1

⇔ x² - 10x - 8 = 0 ⇔ x = 5 ± √33 (thỏa mãn điều kiện)

Với a = 3b ta có √(x+1) = 3√(x² - x + 1) ⇔ x + 1 = 9(x² - x + 1)

⇔ 9x² - 10x + 8 = 0 (phương trình vô nghiệm)

Vậy phương trình có nghiệm là x = 5 ± √33

Câu 8. Chọn B

Phương trình tương đương với 4x² - 4x - |2x-1| - 1 = 0

Đặt t = |2x-1|, t ≥ 0 ⇒ t² = 4x² - 4x + 1 ⇒ 4x² - 4x = t² - 1

Phương trình trở thành t² - 1 - t - 1 = 0 ⇔ t² - t - 2 = 0

⇔

Vì t ≥ 0 ⇒ t = 2 nên |2x - 1| = 2

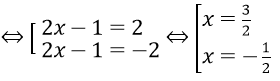
Vậy phương trình có nghiệm là x = 3/2 và x = -1/2

Câu 9. Chọn D

Điều kiện: x ∉ {0; (-1±√5)/2}

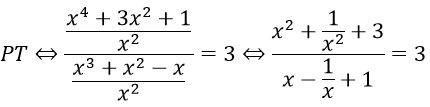
Đặt t = x - 1/x phương trình trở thành (t²+5)/(t+1) = 3

Từ đó phương trình có nghiệm là x = (1±√5)/2; x = 1±√2

Câu 10. Chọn B

Đặt t = x²   (t ≥ 0)

Phương trình (1) thành at² + bt + c = 0  (2)

Phương trình (1) vô nghiệm

⇔ phương trình (2) vô nghiệm hoặc phương trình (2) có 2 nghiệm cùng âm

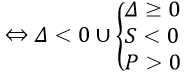
Câu 11. Chọn B

Đặt t = x²  (t ≥ 0)

Phương trình (1) thành t² + t + m = 0 (2)

Phương trình (1)vô nghiệm

⇔ phương trình (2)vô nghiệm hoặc phương trình(2) có 2 nghiệm âm

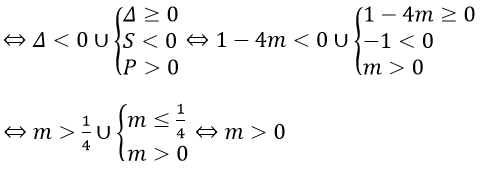
Phương trình có nghiệm ⇔ m ≤ 0

Câu 12. Chọn A

Đặt t = x²/(x-1)

Phương trình(1) thành t² + 2t + a = 0  (2)

Phương trình (1) có đúng 4 nghiệm

⇔ phương trình (2) có 2 nghiệm dương phân biệt

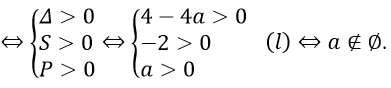
Câu 13. Chọn D

Điều kiện x ≠ 0

Đặt t = x + 1/x suy ra t ≤ -2 hoặc t ≥ 2. Phương trình đã cho trở thành

t² - 2mt - 1 + 2m = 0, phương trình này luôn có hai nghiệm là

t₁ = 1; t₂ = 2m - 1. Theo yêu cầu bài toán ta suy ra

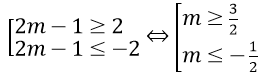
Câu 14. Chọn B

Ta có: x² + 4/x² - 4(x - 2/x) + k - 1 = 0 ⇔(x - 2/x)² - 4(x - 2/x) + k + 3 = 0  (1)

Đặt t = x - 2/x, phương trình trở thành t² - 4t + k + 3 = 0   (2)

Nhận xét : với mỗi nghiệm t của phương trình (2)cho ta hai nghiệm trái dấu của phương trình (1)

Ta có: Δ = 4 - (k+1) = 1 - k

Từ nhận xét trên, phương trình (1) có đúng hai nghiệm lớn hơn 1 khi và chỉ khi

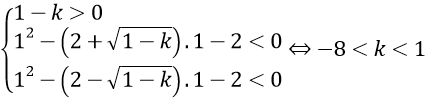
Câu 15. Chọn D

Đặt t = x² + 2x + 4 = (x+1)² + 3 ≥ 3, phương trình trở thành

t² - 2mt + 4m - 1 = 0   (2)

Nhận xét: Ứng với mỗi nghiệm t > 3 của phương trình (2) cho ta hai nghiệm của phương trình (1). Do đó phương trình (1) có đúng hai nghiệm khi phương trình (2) có đúng một nghiệm t > 3