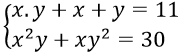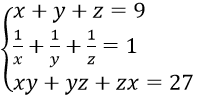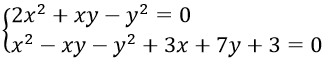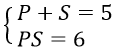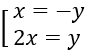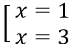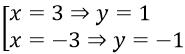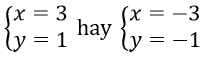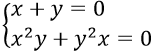Bài tập về các dạng hệ phương trình đặc biệt chọn lọc - Toán lớp 10

---

Bài tập về các dạng hệ phương trình đặc biệt chọn lọc

Với Bài tập về các dạng hệ phương trình đặc biệt chọn lọc Toán lớp 10 tổng hợp 23 bài tập trắc nghiệm có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập các dạng hệ phương trình đặc biệt từ đó đạt điểm cao trong bài thi môn Toán lớp 10.

Câu 1. Để hệ phương trình: 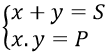có nghiệm , điều kiện cần và đủ là :

A. S² – P < 0          B. S² – P ≥ 0         C. S² – 4P < 0         D. S² – 4P ≥ 0

Câu 2. Cho hệ phương trình 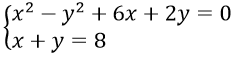. Từ hệ phương trình này ta thu được phương trình sau đây ?

A. x² + 10x + 24 = 0

B. x² + 16x + 20 = 0

C. x² + x – 4 = 0

D. Một kết quá khác

Câu 3. Hệ phương trình

có nghiệm là:

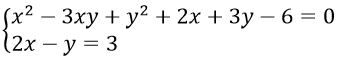
A. (2; 1)          B. (3; 3)          C. (2;1), (3;3)           D. Vô nghiệm

Câu 4. Hệ phương trình 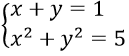có bao nhiêu nghiệm ?

A. 1          B. 2          C. 3          D. 4.

Câu 5. Hệ phương trình

A. có 2 nghiệm (2;3) và (1;5)

B. có 2 nghiệm (2;1) và (3;5)

C. có 1 nghiệm là (5;6)

D. có 4 nghiệm(2;3), (3;2), (1;5), (5;1)

Câu 6. Nghiệm của hệ phương trình

A.(3; 3; 2)          B.(1; 2; 3)          C.(1; 1; 1)          D. (3; 3; 3)

Câu 7. Hệ phương trình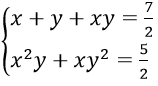 có nghiệm là:

A. (3;2); (-2;1)          B. (0;1), (1;0)          C. (0;2), (2;0)          D. (2;1/2); (1/2;2)

Câu 8. Hệ phương trình 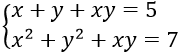có nghiệm là :

A. (2;3) hoặc (3;2)

B. (1;2) hoặc (2;1)

C. (-2;-3) hoặc (-3;-2)

D. (-1;-2) hoặc (-2;-1)

Câu 9. Hệ phương trình 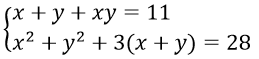có nghiệm là :

A. (3;2), (2;3)

B. (-3;-7), (-7;-3)

C. (3;2); (-3;-7)

D. (3;2), (2;3), (-3;-7), (-7;-3)

Câu 10. Hệ phương trình 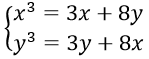có nghiệm là (x; y) với x ≠ 0 và y ≠ 0 là:

A. (-√11;-√11); (√11;√11)

B. (0;√11); (√11;0)

C. (-√11; 0)

D. (√11; 0)

Câu 11. Hãy chỉ ra các cặp nghiệm khác 0 của hệ phương trình:

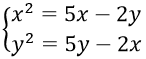
A. (3;3)

B. (2;2), (3;1), (-3;6)

C. (1;1), (2;2), (3;3)

D. (-2;-2), (1;-2), (-6;3)

Câu 12. Hệ phương trình 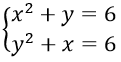có bao nhiêu nghiệm ?

A. 6          B. 4          C. 2          D. 0

Câu 13. Hệ phương trình 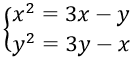có bao nhiêu cặp nghiệm (x; y) ?

A. 3          B. 2          C. 1          D. 0

Câu 14. Cho hệ phương trình 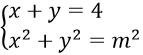. Khẳng định nào sau đây là đúng ?

A. Hệ phương trình có nghiệm với mọi m

B. Hệ phương trình có nghiệm ⇔ |m| ≥ √8

C. Hệ phương trình có nghiệm duy nhất ⇔ |m| ≥ 2

D. Hệ phương trình luôn vô nghiệm

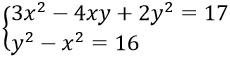
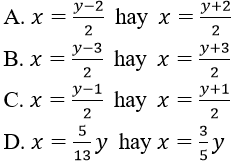
Câu 15. Cho hệ phương trình :. Hệ thức biểu diễn x theo y rút ra từ hệ phương trình là ?

Câu 16. Nghiệm của hệ phương trình: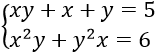 là:

A. (1;2), (2;1)

B. (0;1), (1;0)

C. (0;2), (2;0)

D. (2;1/2), (1/2;2)

Câu 17. Hệ phương trình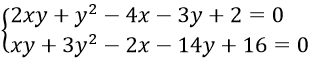có nghiệm là:

A. x bất kỳ, y = 2; x = 1, y = 3

B. x = 3, y = 2; x = 3, y = –1; x = 2, y = –1/2

C. x = 5, y = 2; x = 1, y = 3; x = 1/2, y = 2

D. x = 4, y = 2; x = 3, y = 1; x = 2, y = 1/2

Câu 18. Cho hệ phương trình:

Các cặp nghiệm (x; y) sao cho x, y đều là các số nguyên là:

A. (2;-2), (3;-3)

B. (-2;2), (-3;3)

C. (1;-1), (3;-3)

D. (-1;1), (-4;4)

Câu 19. Tìm số nghiệm của hệ phương trình sau: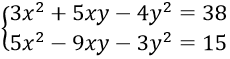

A. 1 nghiệm          B. 2 nghiệm          C. 3 nghiệm          D. 4 nghiệm

Câu 20. Số nghiệm của hệ phương trình: 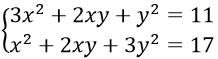là:

A. 1 nghiệm          B. 2 nghiệm          C. 3 nghiệm          D. 4 nghiệm

Câu 21. Cho hệ phương trình 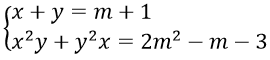và các mệnh đề:

(I) Hệ có vô số nghiệm khi = -1

(II) Hệ có nghiệm khi > 3/2

(III) Hệ có nghiệm với mọi

Các mệnh đề nào đúng ?

A. Chỉ (I)           B. Chỉ (II)          C. Chỉ (III)          D. Chỉ (I) và (III)

Câu 22. Với giá trị nào của m thì hệ: 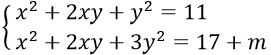có nghiệm

A. m ≥ -6           B. m ≤ -6           C. m < -6           D. m ≥ 6

Câu 23. Hệ phương trình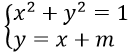 có đúng 1 nghiệm khi và chỉ khi :

A. m = √2

B. m = -√2

C. m = √2 hoặc m = -√2

D. m tùy ý

 

Đáp án và hướng dẫn giải

Câu	1	2	3	4	5	6	7	8	9	10	11
Đáp án	D	D	C	B	D	D	D	B	D	A	A

Câu	12	13	14	15	16	17	18	19	20	21	22	23
Đáp án	C	B	B	D	A	A	C	B	D	D	A	C

Câu 1. Chọn D

Ta có : x, y là nghiệm phương trình X² - SX + P = 0

Hệ phương trình có nghiệm khi Δ = S² - 4P ≥ 0

Câu 2. Chọn D

Ta có : y = 8-x ⇒ x² - (8-x)² + 6x + 2(8-x) = 0 ⇒ 20x - 48 = 0

Câu 3. Chọn C

Ta có : y = 2x-3 ⇒ x² - 3x(2x-3) + (2x-3)² + 2x + 3(2x-3) - 6 = 0

⇒ -x² + 5x - 6 = 0 ⇒ x = 2; x = 3

Với x = 2 ⇒ y = 1

Với x = 3 ⇒ y = 3

Câu 4. Chọn B.

Ta có : y = 1-x ⇒ x² + (1-x)² = 5 ⇒ 2x² - 2x - 4 = 0 ⇒ x = -1; x = 2

Vậy hệ phương trình đã cho có hai nghiệm

Câu 5. Chọn D

Đặt S = x+y, P = xy (S² - 4P ≥ 0)

Hệ phương trình tương đương

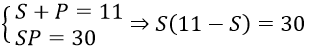
⇒-S² + 11S - 30 = 0 ⇒ S = 5; S = 6

Khi S = 5 thì P = 6 suy ra hệ có nghiệm (2;3),(3;2)

Khi S = 6 thì P = 5 suy ra hệ có nghiệm (1;5),(5;1)

Câu 6. Chọn D

Ta có : 1/x + 1/y + 1/z = 1 ⇔ xy + yz + zx = xyz ⇒ xyz = 27

⇒ x, y, z là nghiệm của phương trình X³ - 9X² + 27X - 27 = 0 ⇔ X = 3

Vậy hệ phương trình có nghiệm (3; 3; 3)

Câu 7. Chọn D

Đặt S = x+y, P = xy (S² - 4P ≥ 0)

Ta có :

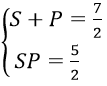
⇒ S, P là nghiệm của phương trình X² - (7/2)X + 5/2 = 0

⇔ X = 1; X = 5/2

Khi S = 1; P = 5/2 (loại)

Khi S = 5/2; P = 1 thì x, y là nghiệm của phương trình X² - (5/2)X + 1 = 0

⇔ X = 2; X = 1/2

Vậy hệ phương trình có nghiệm (2;1/2); (1/2;2)

Câu 8. Chọn B

Đặt S = x+y, P = xy (S² - 4P ≥ 0)

Ta có

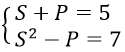
⇒ S² - (5-S) = 7 ⇒ S² + S - 12 = 0 ⇒ S = 3; S = -4

Khi S = 3 ⇒ P = 2 thì x, y là nghiệm của phương trình X² - 3X + 2 = 0

⇔ X = 1; X = 2

Khi S = 2 ⇒ P = 3 (loại)

Vậy hệ có nghiệm là (1; 2) hoặc (2; 1)

Câu 9. Chọn D

Đặt S = x+y, P = xy (S² - 4P ≥ 0)

Ta có

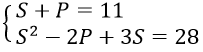
⇒ S² - 2(11-S) + 3S = 28 ⇒ S² + 5S - 50 = 0 ⇒ S = 5; S = -10

Khi S = 5 ⇒ P = 6 thì x, y là nghiệm của phương trình X² - 5X + 6 = 0

⇔ X = 2; X = 3

Khi S = -10 ⇒ P = 21 thì x, y là nghiệm của phương trình

X² + 10X + 21 = 0 ⇔ X = -3; X = -7

Vậy hệ có nghiệm (3;2), (2;3), (-3;-7), (-7;-3)

Câu 10. Chọn A

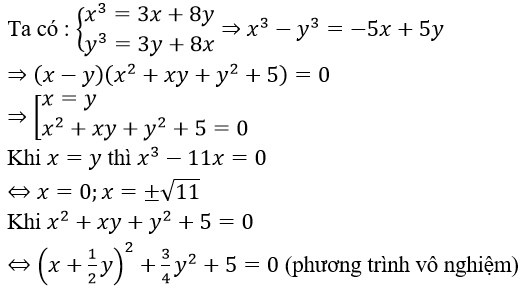
Vậy hệ có nghiệm (-√11;-√11); (√11;√11).

Câu 11. Chọn A

Ta có :

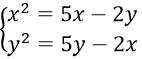
⇒ x² - y² = 7x - 7y ⇒ (x-y)(x+y-7) = 0

Khi x = y thì x² - 3x = 0 ⇔ x = 0; x = 3

Khi y = 7-x thì x² - 7x + 14 = 0 (phương trình vô nghiệm)

Vậy hệ phương trình có nghiệm (3; 3)

Câu 12. Chọn C

Ta có :

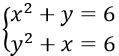
⇒ x² - y² + y - x = 0 ⇒ (x - y)(x + y - 1) = 0

Khi x = y thì x² + x - 6 = 0 ⇔ x = -3; x = 2

Khi y = 1 - x thì x² - x + 7 = 0 (phương trình vô nghiệm)

Vậy hệ phương trình đã cho có hai nghiệm (-3; -3) và (2; 2)

Câu 13. Chọn B

Ta có :

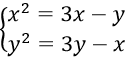
⇒x² - y² = 4x - 4yx ⇒ (x-y)(x+y-1) = 0

Khi x = y thì x² - 2x = 0 ⇔ x = 0; x = 2

Khi y = 4-x thì x² - 4x + 4 = 0 ⇔ x = 2

Vậy hệ phương trình có 2 nghiệm (0;0), (2;2)

Câu 14. Chọn B

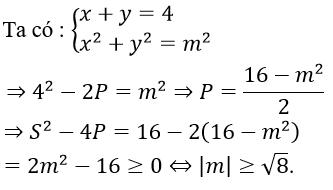
Câu 15. Chọn D

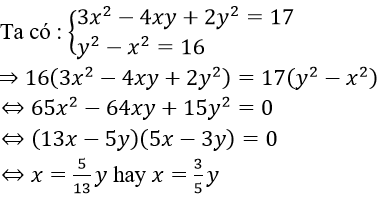
Câu 16. Chọn A

Đặt S = x+y, P = xy (S² - 4P ≥ 0)

Ta có:

⇒ S, P là nghiệm của phương trình X² - 5X + 6 = 0 ⇔ X = 2; X = 3

Khi S = 2, P = 3 (loại)

Khi S = 3, P = 2 thì x, y là nghiệm phương trình X² - 3X + 2 = 0

⇔ X = 1; X = 2

Vậy nghiệm của hệ là (1;2), (2;1)

Câu 17. Chọn A

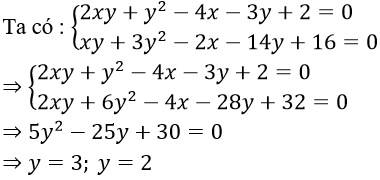
Khi y = 3 thì x = 1

Khi y = 2 thì x tuỳ ý

Câu 18. Chọn C

Phương trình (1)⇔ (x+y)(2x-y) = 0 ⇔

Trường hợp 1: x = -y thay vào (2) ta được x² - 4x + 3 = 0 ⇔

Suy ra hệ phương trình có hai nghiệm là (1; -1), (3; -3)

Trường hợp 2: 2x = y thay vào (2) ta được -5x² + 17x + 3 = 0 phương trình nay không có nghiệm nguyên

Vậy các cặp nghiệm (x; y) sao cho x, y đều là các số nguyên là (1; -1) và (3; -3)

Câu 19. Chọn B

Ta thấy x = 0 không thoả hệ phương trình

Xét x ≠ 0. Đặt x = ky và thay vào hệ ta được

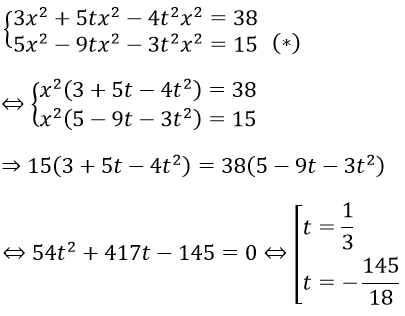
Với t = 1/3 thì (*) ⇔ x² = 9 ⇔

Với t = -145/18 thì (*) ⇔ x² = -15.108/12655 : Phương trình vô nghiệm

Vậy

Câu 20. Chọn D

Dễ thấy x = 0 không thoả hệ

Với x ≠ 0, đặt y = tx , thay vào hệ ta được

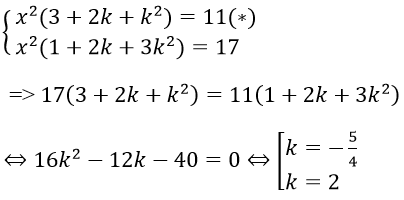
Thay vào (*) ta được:

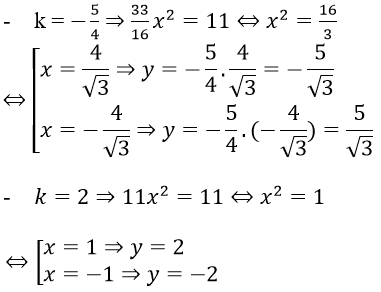
Vậy hệ phương trình có nghiệm (x;y) là (-4/√3,5/√3); (4/√3,-5/√3); (1;2); (-1;-2)

Câu 21. Chọn D

Khi m = -1 thì hệ trở thành

⇒ hệ có vô số nghiệm ⇒ (I) đúng

Ta có:

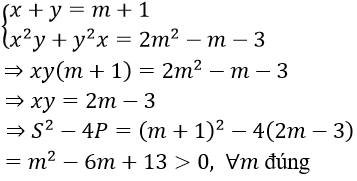
Câu 22. Chọn A

Dễ thấy x = 0 không thoả hệ

Với x ≠ 0, đặt y = tx , thay vào hệ ta được

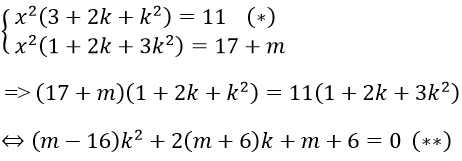
Ta có: 3 + 2k + k² = (k+1)² + 2 > 0, ∀k ⇒ (*) luôn có nghiệm x với mọi k do đó hệ ban đầu có nghiệm khi và chỉ khi phương trình (**) có nghiệm ẩn k

Với m = 16: Phương trình (**) trở thành 44k + 88 = 0 ⇔ k = -2

Vậy m = 16 thỏa mãn

Với m ≠ 16: Phương trình (**) có nghiệm ⇔Δ'_k ≥ 0

⇔(m+6)² - (m-16)(m+6) ≥ 0 ⇔ 22(m+6) ≥ 0 ⇔ m ≥ -6

Vậy hệ phương trình có nghiệm khi và chỉ khi m ≥ -6

Câu 23. Chọn C

Ta có : x² + (x+m)² = 1 ⇔ 2x² + 2mx + m² - 1 = 0   (*)

Hệ phương trình có đúng 1 nghiệm khi phương trình (*) có đúng 1 nghiệm

⇒ Δ' = m² - 2m² + 2 = 0 ⇔ m = ±√2