Bài tập tổng hợp về hàm số bậc nhất lớp 10 chọn lọc - Toán lớp 10

Bài tập tổng hợp về hàm số bậc nhất lớp 10 chọn lọc

Với Bài tập tổng hợp về hàm số bậc nhất lớp 10 chọn lọc Toán lớp 10 tổng hợp 10 bài tập có lời giải chi tiết sẽ giúp học sinh ôn tập, biết cách làm dạng bài tập hàm số từ đó đạt điểm cao trong bài thi môn Toán lớp 10.

Bài 1: Cho hàm số bậc nhất có đồ thị là đường thẳng d. Tìm hàm số đó biết:

a) d đi qua A(1; 1), B (3; -2)

b) d đi qua C (2; -2) và song song với Δ: x - y + 1 = 0

c) d đi qua M(1; 2) và cắt hai tia Ox, Oy tại P, Q sao cho tam giác OPQ cân tại O.

d) d đi qua N(1; -1) và d ⊥ d' với d':y = -x + 3.

Bài 2: Tìm m để ba đường thẳng d: y = 2x,d': y = -x + 6,

d": y = m²x + 5m + 3 phân biệt đồng quy.

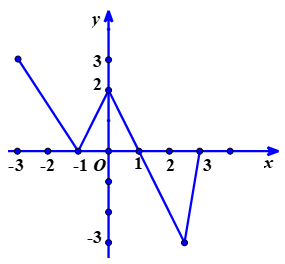
Bài 3: Cho đồ thị hàm số có đồ thị (C) (hình vẽ)

a) Hãy lập bảng biến thiên của hàm số trên [-3;3]

b) Tìm giá trị lớn nhất và nhỏ nhất của hàm số trên [-2;2]

Bài 4: Vẽ đồ thị hàm số y = 2x - 3. Từ đó suy ra đồ thị của:

(C₁ ): y = 2|x| - 3

(C₂ ): y = |2x - 3|

(C₃ ): y = |2|x| - 3|

Bài 5: a) Lập bảng biến thiên của hàm số:

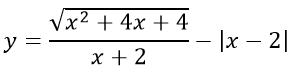
b) Biện luận số giao điểm của đồ thị hàm số trên với đường thẳng y = m theo m.

Bài 6: Cho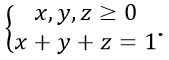Chứng minh:

0 ≤ xy + yz + zx - 2xyz ≤ 7/27

Bài 7: Chứng minh rằng với ∀ m ≤ 1 thì x² - 2(3m-1)x + m + 3 ≥ 0 ∀ x ∈ [1;+∞)

Đáp án và hướng dẫn giải

Bài 1: Gọi hàm số cần tìm là y = ax + b, a ≠ 0

a) Vì A ∈ d,B ∈ d nên ta có hệ phương trình:

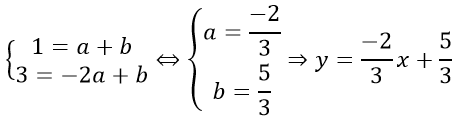
b) Ta có Δ:y = x + 1. Vì d // Δ nên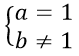

Mặt khác C ∈ d ⇒ -2 = 2a + b ⇒ b = -4

Vậy hàm số cần tìm là y = x – 4.

c) Đường thẳng d cắt tia Ox tại P(-b/a; 0) và cắt tia Oy tại Q(0; b) với a < 0; b > 0.

Tam giác OPQ cân tại O ⇔ OP = OQ

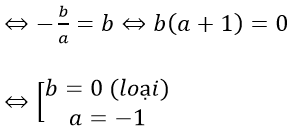
Ta có: M ∈ d ⇒ 2 = a + b ⇒ b = 3

Vậy hàm số cần tìm là y = -x + 3.

d) Đường thẳng d đi qua N (1; -1) nên -1 = a + b

Và d ⊥ d' ⇒ a = 1 suy ra b = -2.

Vậy hàm số cần tìm là y = x – 2.

Bài 2: Tọa độ giao điểm (nếu có) của hai đường thẳng d, d’ là nghiệm của hệ phương trình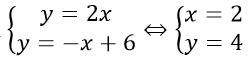suy ra d, d’ cắt nhau tại M (2; 4)

Vì ba đường thẳng d, d’, d’’ đồng quy nên M ∈ d" ta có:

4 = 2m² + 5m + 3 ⇔ 2m² + 5m - 1 = 0

⇔

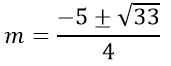
Dễ thấy với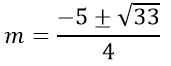ba đường thẳng đó phân biệt và đồng quy

Vậy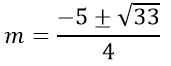là giá trị cần tìm.

Bài 3:

a) Bảng biến thiên của hàm số trên [-3; 3]

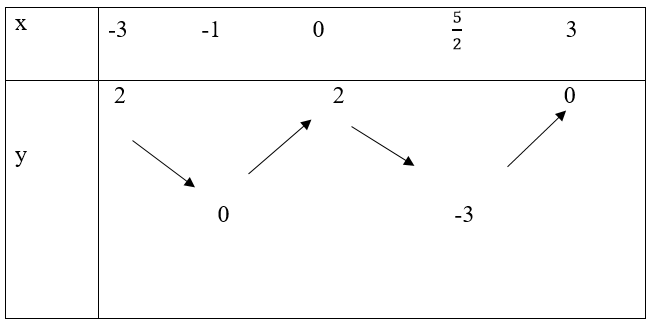
b) Dựa vào đồ thị hàm số đã cho ta có:

Bài 4: Đồ thị hàm số y = 2x – 3 đi qua A(0; -3), B (2; 1) ta gọi là (C)

+ Khi đó đồ thị hàm số (C₁ ): y = 2|x| - 3 là phần được xác định như sau

Ta giữ nguyên đồ thị (C) ở bên phải trục tung; lấy đối xứng đồ thị (C) ở phần bên phải trục tung qua trục tung.

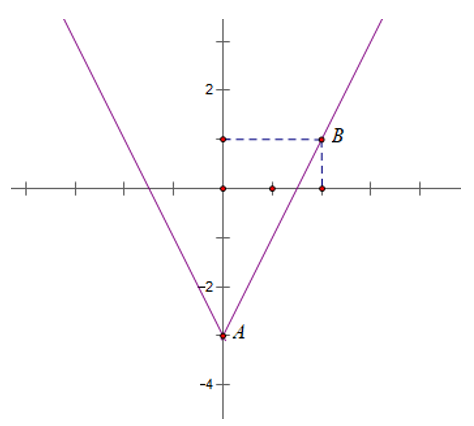
+ (C₂ ): y = |2x - 3| là phần đồ thị (C) nằm phía trên trục hoành và đồ thị lấy đối xứng qua trục hoành của phần nằm trên trục hoành của(C).

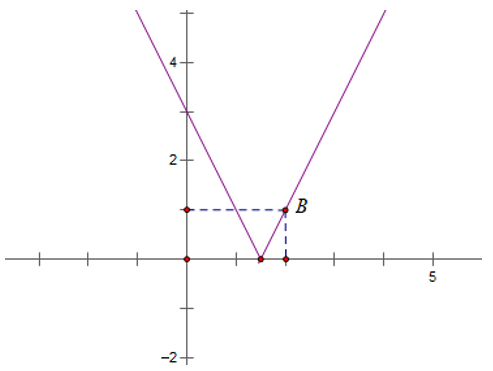
+ (C₃ ): y = |2|x| - 3| là phần đồ thị (C₁ ) nằm phái trên trục hoành và đồ thị lấy đối xứng qua trục hoành của phần nằm trên trục hoành của (C₁ ).

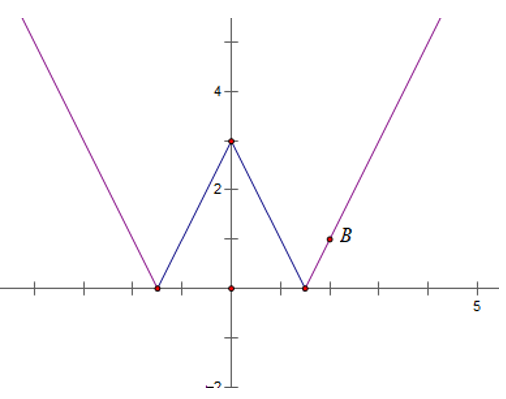
Bài 5:

a) Ta có

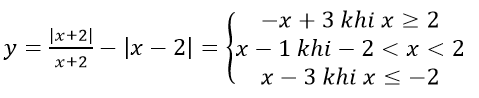
Bảng biến thiên:

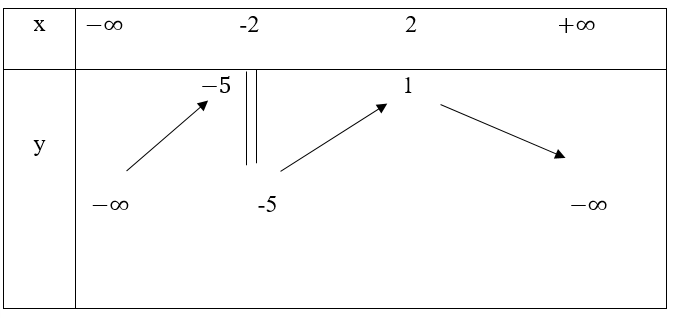
b) Dựa vào bảng biến thiên của hàm số: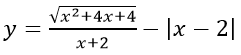ta có số giao điểm của nó với đường thẳng y = m như sau:

Với m > 1 thì có không giao điểm

Với m = 1 thì có một giao điểm

Với -5 < m < 1 thì có hai giao điểm

Với m < -5 thì có một giao điểm.

Bài 6: Từ giả thiết ta có x,y,z ∈ [0;1]

⇒ xy + yz + zx - 2xyz = xy + yz(1-x) + zx(1-y) ≥ 0

Cũng từ giả thiết ta suy ra:

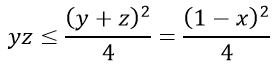
Mặt khác ta lại có

xy + yz + zx - 2xyz ≤ 7/27 ⇔ f(yz) = (1-2x)yz + x(1-x) - 7/27 ≤ 0 (2)

Khi đó ta thấy rằng

Nếu x = 1/2 khi đó BĐT (2) thành (-1)/108 (hiển nhiên đúng).

Nếu x ≠ 1/2 thì f(yz) là hàm số bậc nhất. Do đó để chứng minh f(yz) ≤ 0 ta chỉ cần

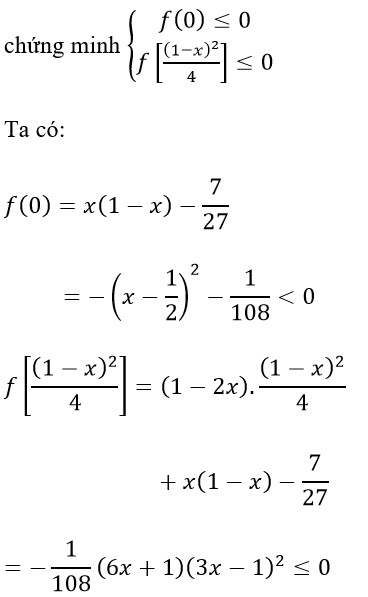
Vậy f(yz) ≤ 0, ta có điều phải chứng minh.

Bài 7:

Ta có x² - 2(3m-1)x + m + 3 ≥ 0

⇔ f(m) = (-6x+1)m + x² + 2x + 3 ≥ 0

Ta thấy f(m) là hàm số bậc nhất có hệ số của m là -6x + 1 < 0 (do x ∈ [1;+∞)). Khi đó: f(m) là hàm nghịch biến ⇒ f(m) ≥ f(1) với ∀ m ≤ 1. Tức là ta có :

x² - 2(3m-1)x + m + 3 ≥ (x-2)² ≥ 0 (đúng với ∀ x ∈ [1;+∞)).